某玩具由一个圆形区域和一个扇形区域组成,如图,在⊙O1和扇形O2CD中,⊙O1与O2C、O2D分别相切于A、B,∠CO2D=60°,直线O1O2与⊙O1、扇形O2CD分别交于E、F两个点,EF=24cm,设⊙O1的半径为xcm,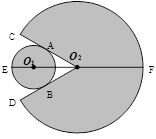
(1)用含x的代数式表示扇形O2CD的半径;
(2)若⊙O1和扇形O2CD两个区域的制作成本分别为0.45元/cm2和0.06/cm2元,当⊙O1的半径为多少时,该玩具成本最小?
如图, 的顶点 、 分别在 轴, 轴上, ,且 的面积为8.
(1)直接写出 、 两点的坐标;
(2)过点 、 的抛物线 与 轴的另一个交点为点 .
①若 是以 为腰的等腰三角形,求此时抛物线的解析式;
②将抛物线 向下平移4个单位后,恰好与直线 只有一个交点 ,求点 的坐标.

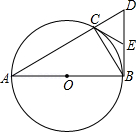
如图,已知 内接于 , 为 的直径, ,交 的延长线于点 .
(1) 为 的中点,连接 ,求证: 是 的切线;
(2)若 ,求 的大小.
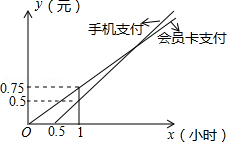
为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额 (元 与骑行时间 (时 之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额 (元 与骑行时间 (时 的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.
衡阳市城市标志来雁塔坐落在衡阳市雁峰公园内,如图,为了测量来雁塔的高度,在 处用高为1.5米的测角仪 ,测得塔顶 的仰角为 ,再向塔身前进10.4米,又测得塔顶 的仰角为 ,求来雁塔的高度.(结果精确到0.1米)

为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为: .唐诗; .宋词; .论语; .三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.