已知数列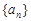 满足:
满足: ,数列
,数列 满足
满足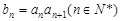 .
.
(1)若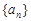 是等差数列,且
是等差数列,且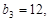 求
求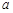 的值及
的值及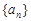 的通项公式;
的通项公式;
(2)若 是公比为
是公比为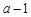 的等比数列,问是否存在正实数
的等比数列,问是否存在正实数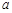 ,使得数列
,使得数列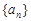 为等比数列?若存在,求出
为等比数列?若存在,求出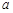 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)若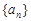 是等比数列,求
是等比数列,求 的前
的前 项和
项和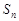 (用n,
(用n,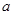 表示).
表示).
(本小题满分12分)数列 满足:
满足: ,
, 且
且
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)求数列 的前
的前 项和
项和 .
.
(本小题满分12分)直三棱柱

 是
是 的中点.
的中点. 
(Ⅰ)求证: ;
;
(Ⅱ)求证: .
.
(本小题满分12分)为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C万元与隔热层厚度 cm满足关系:
cm满足关系: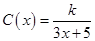 (
(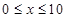 ,
,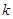 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(Ⅰ)求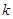 的值及
的值及 的表达式;
的表达式;
(Ⅱ)隔热层修建多厚时,总费用 达到最小?并求最小值.
达到最小?并求最小值.
(本小题满分12分)已知向量 ,
, ,函数
,函数 .
.
(Ⅰ)求函数 的对称中心;
的对称中心;
(Ⅱ)在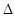
 中,
中,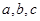 分别是角
分别是角 的对边,且
的对边,且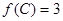 ,
, ,
,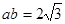 ,且
,且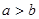 ,求
,求 的值.
的值.
(本小题满分10分)选修 :不等式选讲
:不等式选讲
已知函数 ,
,
(1)当 时,求不等式
时,求不等式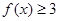 的解集;
的解集;
(2)若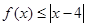 的解集包含
的解集包含 ,求
,求 的取值范围.
的取值范围.