(本小题满分12分)直三棱柱

 是
是 的中点.
的中点. 
(Ⅰ)求证: ;
;
(Ⅱ)求证: .
.
【2015高考天津,文15】(本小题满分13分)设甲、乙、丙三个乒乓球协会的运动员人数分别为27,9,18,先采用分层抽样的方法从这三个协会中抽取6名运动员参加比赛.
(Ⅰ)求应从这三个协会中分别抽取的运动员人数;
(Ⅱ)将抽取的6名运动员进行编号,编号分别为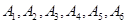 ,从这6名运动员中随机抽取2名参加双打比赛.
,从这6名运动员中随机抽取2名参加双打比赛.
(ⅰ)用所给编号列出所有可能的结果;
(ⅱ)设A为事件“编号为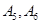 的两名运动员至少有一人被抽到”,求事件A发生的概率.
的两名运动员至少有一人被抽到”,求事件A发生的概率.
【2015高考四川,文17】一辆小客车上有5个座位,其座位号为1,2,3,4,5,乘客P1,P2,P3,P4,P5的座位号分别为1,2,3,4,5,他们按照座位号顺序先后上车,乘客P1因身体原因没有坐自己号座位,这时司机要求余下的乘客按以下规则就坐:如果自己的座位空着,就只能坐自己的座位.如果自己的座位已有乘客就坐,就在这5个座位的剩余空位中选择座位.
(Ⅰ)若乘客P1坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
| 乘客 |
P1 |
P2 |
P3 |
P4 |
P5 |
| 座位号 |
3 |
2 |
1 |
4 |
5 |
| 3 |
2 |
4 |
5 |
1 |
|
(Ⅱ)若乘客P1坐到了2号座位,其他乘客按规则就坐,求乘客P1坐到5号座位的概率.
【2015高考陕西,文19】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
| 日期 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 天气 |
晴 |
雨 |
阴 |
阴 |
阴 |
雨 |
阴 |
晴 |
晴 |
晴 |
阴 |
晴 |
晴 |
晴 |
晴 |
| 日期 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
| 天气 |
晴 |
阴 |
雨 |
阴 |
阴 |
晴 |
阴 |
晴 |
晴 |
晴 |
阴 |
晴 |
晴 |
晴 |
雨 |
(Ⅰ)在4月份任取一天,估计西安市在该天不下雨的概率;
(Ⅱ)西安市某学校拟从4月份的一个晴天开始举行连续两天的运动会,估计运动会期间不下雨的概率.
【2015高考山东,文16】某中学调查了某班全部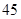 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
| 参加书法社团 |
未参加书法社团 |
|
| 参加演讲社团 |
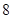 |
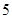 |
| 未参加演讲社团 |
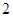 |
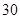 |
(1)从该班随机选 名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的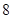 名同学中,有5名男同学
名同学中,有5名男同学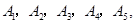
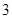 名女同学
名女同学 现从这
现从这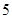 名男同学和
名男同学和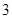 名女同学中各随机选
名女同学中各随机选 人,求
人,求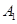 被选中且
被选中且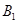 未被选中的概率.
未被选中的概率.
【2015高考湖南,文16】(本小题满分12分)某商场举行有奖促销活动,顾客购买一定金额的商品后即可抽奖,抽奖方法是:从装有2个红球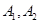 和1个白球
和1个白球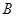 的甲箱与装有2个红球
的甲箱与装有2个红球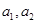 和2个白球
和2个白球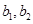 的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖。
的乙箱中,各随机摸出1个球,若摸出的2个球都是红球则中奖,否则不中奖。
(Ⅰ)用球的标号列出所有可能的摸出结果;
(Ⅱ)有人认为:两个箱子中的红球比白球多,所以中奖的概率大于不中奖的概率,你认为正确吗?请说明理由。