【2015高考陕西,文19】随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
| 日期 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 天气 |
晴 |
雨 |
阴 |
阴 |
阴 |
雨 |
阴 |
晴 |
晴 |
晴 |
阴 |
晴 |
晴 |
晴 |
晴 |
| 日期 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
| 天气 |
晴 |
阴 |
雨 |
阴 |
阴 |
晴 |
阴 |
晴 |
晴 |
晴 |
阴 |
晴 |
晴 |
晴 |
雨 |
(Ⅰ)在4月份任取一天,估计西安市在该天不下雨的概率;
(Ⅱ)西安市某学校拟从4月份的一个晴天开始举行连续两天的运动会,估计运动会期间不下雨的概率.
如图,梯形 的顶点
的顶点 与顶点
与顶点 分别在平面
分别在平面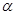 的两侧,且梯形的两边
的两侧,且梯形的两边 与
与 分别与
分别与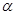 交于
交于 两点;梯形的另两条边
两点;梯形的另两条边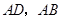 的延长线分别与
的延长线分别与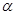 交于
交于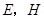 两点,求证:
两点,求证: 四点共线.
四点共线.
已知 的三个顶点
的三个顶点 ,
,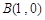 ,
,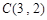 ,其外接圆为圆
,其外接圆为圆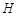 .
.
(1)求圆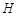 的方程;
的方程;
(2)若直线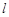 过点
过点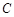 ,且被圆
,且被圆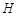 截得的弦长为2,求直线
截得的弦长为2,求直线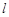 的方程;
的方程;
(3)对于线段 上的任意一点
上的任意一点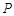 ,若在以
,若在以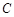 为圆心的圆上都存在不同的两点
为圆心的圆上都存在不同的两点 ,使得点
,使得点 是线段
是线段 的中点,求圆
的中点,求圆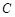 的半径
的半径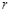 的取值范围.
的取值范围.
【改编】如图,已知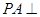 面
面 ,
, ,
, ;
;
(1)在线段 上找一点M,使
上找一点M,使 面
面 。
。
(2)求由面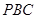 与面
与面 所成角的二面角的正切值。
所成角的二面角的正切值。
已知圆 .
.
(Ⅰ)写出圆C的标准方程,并指出圆心坐标和半径大小;
(Ⅱ)是否存在斜率为 的直线m,使m被圆C截得的弦为AB,且
的直线m,使m被圆C截得的弦为AB,且 (
( 为坐标原点).若存在,求出直线m的方程; 若不存在,说明理由.
为坐标原点).若存在,求出直线m的方程; 若不存在,说明理由.
如图,四棱锥 的底面为矩形,
的底面为矩形, ,
, ,
,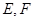 分别是
分别是 的中点,
的中点, .
.
(Ⅰ)求证: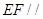 平面
平面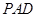 ;
;
(Ⅱ)求证:平面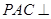 平面
平面 .
.