已知圆M: 与
与 轴相切。
轴相切。
(1)求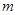 的值;
的值;
(2)求圆M在 轴上截得的弦长;
轴上截得的弦长;
(3)若点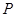 是直线
是直线 上的动点,过点
上的动点,过点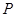 作直线
作直线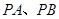 与圆M相切,
与圆M相切, 为切点。求四边形
为切点。求四边形 面积的最小值。
面积的最小值。
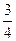
(1)设 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求 的分布列及
的分布列及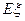 ;
;
(2)设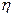 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数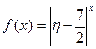 在定义域内单调递减”为事件
在定义域内单调递减”为事件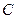 ,求事件
,求事件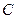 的概率
的概率

侧棱PA=PD= ,底面ABCD为直角梯形,其中
,底面ABCD为直角梯形,其中
BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
(1)求证:PO⊥平面ABCD;
(2)求异面直线PB与CD所成角的余弦值;
(3)线段AD上是否存在点Q,使得它到平面PCD的距离为 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
数列{an}的前n项和记为Sn,
(1)求{an}的通项公式;
(2)等差数列{bn}的各项为正,其前n项和为Tn,且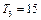 ,又
,又 成等比数列,求Tn
成等比数列,求Tn
设a为实数,记函数 的最大值为g(a).
的最大值为g(a).
(1)设t= ,求t的取值范围,并把f(x)表示为t的函数m(t);
,求t的取值范围,并把f(x)表示为t的函数m(t);
(2)求g(a);
(3)试求满足 的所有实数a.
的所有实数a.
设函数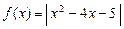 .
.
(1)在区间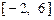 上画出函数
上画出函数 的图像;
的图像;
(2)设集合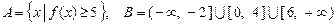 . 试判断集合
. 试判断集合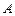 和
和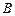 之间的关系,并给出证明;
之间的关系,并给出证明;
(3)当 时,求证:在区间
时,求证:在区间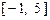 上,
上, 的图像位于函数
的图像位于函数 图像的
图像的
上方.