如图，四边形ABCD是矩形，AB＝3，AD＝4，直线PS分别交AB、CD的延长线于P、S，交BC、AC、AD于Q、E、R，BP＝1，DS＝2．
（1）写出图中相似三角形（不含全等三角形）；
（2）请找出图中除AB＝CD、BC＝AD以外的相等线段，并证明你的判断．
（3）求四边形ABQR与四边形CQRD的面积比．
如图，直线l1的解析式为y=﹣3x+3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C．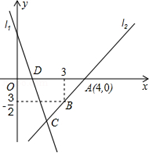
（1）求直线l2的解析表达式；
（2）求△ADC的面积；
（3）若点P为第一象限上的一点，且以A，C，D，P为顶点的四边形为平行四边形，试求点P的坐标．
如图，在正方形ABCD中，点E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在正方形ABCD的内部，延长AF交CD于点G．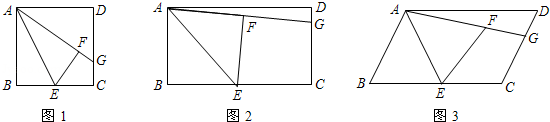
（1）猜想并证明线段GF与GC的数量关系；
（2）若将图1中的正方形改成矩形，其它条件不变，如图2，那么线段GF与GC之间的数量关系是否改变？请证明你的结论；
（3）若将图1中的正方形改成平行四边形，其它条件不变，如图3，那么线段GF与GC之间的数量关系是否会改变？请证明你的结论．
某工厂生产一种产品，当生产数量至少为10吨，但不超过50吨时，每吨的成本y（万元/吨）与生产数量x（吨）的函数关系式如图所示．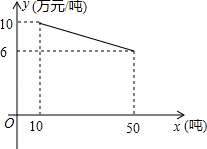
（1）求y关于x的函数解析式，并写出自变量的取值范围；
（2）当每吨成本为9万元时，求该产品的生产数量．
滨湖区举行“我的中国梦”演讲比赛，某校中学组根据初赛成绩在七2014-2015学年八年级分别选出10名同学参加比赛，这些选手的决赛成绩如图所示：
（1）请你把下面的表格填写完整：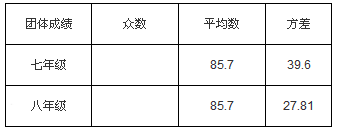
（2）考虑平均数与方差，你认为哪个年级的团体成绩更好些；
（3）假设在每个年级的选手中分别选出3人参加总决赛，你认为哪个年级的实力更强一些，请说明理由．
如图，已知△ABC中，AB=AC，E，D，F分别是边AB，BC，AC的中点．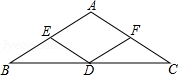
（1）求证：四边形AEDF是菱形；
（2）若∠B=30°，BC=4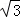
，求四边形AEDF的周长．