如图,已知菱形 ,其边长为2,
,其边长为2, ,
, 绕着
绕着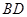 顺时针旋转
顺时针旋转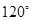 得到
得到 ,
, 是
是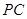 的中点.
的中点.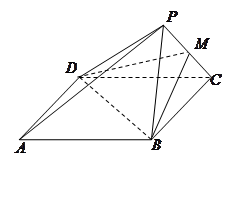
(1)求证: 平面
平面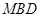 ;
;
(2)求直线 与平面
与平面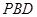 所成角的正弦值.
所成角的正弦值.
已知 在x=2时有极大值6,在x=1时有极小值.
在x=2时有极大值6,在x=1时有极小值.
⑴ 求 的值;
的值;
⑵ 求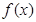 在区间
在区间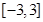 上的最大值和最小值.
上的最大值和最小值.
对某校高一年级学生参加社区服务次数进行统计,随机抽取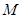 名学生作为样本,得到这
名学生作为样本,得到这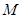 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 |
频数 |
频率 |
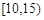 |
10 |
0.25 |
 |
25 |
 |
 |
 |
 |
 |
2 |
0.05 |
| 合计 |
M |
1 |

⑴求出表中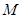 、
、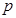 及图中
及图中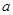 的值;
的值;
⑵若该校高一学生有720人,试估计他们参加社区服务的次数在区间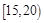 内的人数;
内的人数;
⑶在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间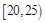 内的概率.
内的概率.
(本小题满分18分)已知函数 ,
,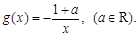
(Ⅰ)若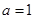 ,求函数
,求函数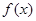 的极值;
的极值;
(Ⅱ)设函数 ,求函数
,求函数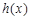 的单调区间;
的单调区间;
(Ⅲ)若在 (
(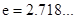 )上存在一点
)上存在一点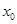 ,使得
,使得
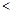
 成立,求
成立,求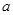 的取值范围.
的取值范围.
(本小题满分18分)设数列{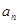 }的前
}的前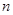 项和为
项和为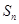 ,且满足
,且满足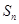 =2-
=2-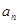 ,(
,(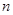 =1,2,3,…)
=1,2,3,…)
(Ⅰ)求数列{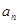 }的通项公式;
}的通项公式;
(Ⅱ)若数列{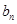 }满足
}满足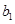 =1,且
=1,且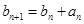 ,求数列{
,求数列{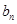 }的通项公式;
}的通项公式;
(Ⅲ)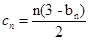 ,求
,求 的前
的前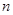 项和
项和
(本小题满分15分)如图,在四棱锥 中,底面
中,底面 是正方形,侧棱
是正方形,侧棱 底面
底面 ,
,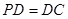 ,
,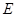 是
是 的中点,作
的中点,作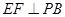 交
交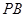 于点
于点

(1)证明: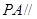 平面
平面 .
.
(2)证明: 平面
平面 .
.
(3)求二面角 的大小.
的大小.