把一边长为40cm的正方形硬纸板,进行适当的剪裁,折成一个长方形盒子(纸板的厚度忽略不计)。
(1)如图1,若在正方形硬纸板的四角各剪一个同样大小的正方形,将剩余部分折成一个无盖的长方形盒子。
①要使折成的长方形盒子的底面积为484cm2,那么剪掉的正方形的边长为多少?
②折成的长方形盒子的侧面积是否有最大值?如果有,求出这个最大值及此时剪掉的正方形的边长;如果没有,请说明理由。
(2)如图2在正方形硬纸板上剪掉一些矩形(图2中阴影为剪去部分),将剩余部分折成一个有盖的长方形盒子,若折成的一个长方形盒子的表面积为550cm2,求此时长方形盒子的长、宽、高。
(8分)比较正五边形与正六边形,可以发现它们的相同点和不同点.例如: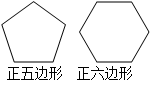
它们的一个相同点:正五边形的各边相等,正六边形的各边也相等.
它们的一个不同点:正五边形不是中心对称图形,正六边形是中心对称图形.
请你再写出它们的两个相同点和不同点:
相同点:
①;
②.
不同点:
①;
②.
(8分)在社区全民健身活动中,父子俩参加跳绳比赛.相同时间内父亲跳180个,儿子跳210个.已知儿子每分钟比父亲多跳20个,父亲、儿子每分钟各跳多少个?
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
(1)求此抛物线的函数表达式;
(2)设E是y轴右侧抛物线上异于点B的一个动点,过点E作x轴的平行线交抛物线于另一点F,过点F作FG垂直于x轴于点G,再过点E作EH垂直于x轴于点H,得到矩形EFGH.则在点E的运动过程中,当矩形EFGH为正方形时,求出该正方形的边长;
(3)在抛物线上是否存在异于B、C的点M,使△MBC中BC边上的高为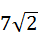 ?若存在,求出点M的坐标;若不存在,请说明理由.
?若存在,求出点M的坐标;若不存在,请说明理由.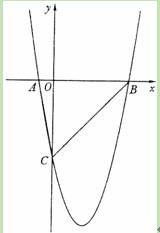
已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,⊙O经过B、D两点,过点B作BK⊥AC,垂足为K.过D作DH∥KB,DH分别与AC、AB、⊙O及CB的延长线相交于点E、F、G、H.
(1)求证:AE=CK;
(2)如果AB=a,AD=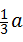 (a为大于零的常数),求BK的长:
(a为大于零的常数),求BK的长:
(3)若F是EG的中点,且DE=6,求⊙O的半径和GH的长.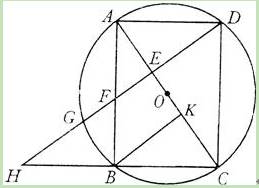
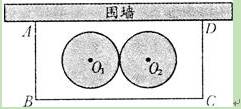
某学校要在围墙旁建一个长方形的中药材种植实习苗圃,苗圃的一边靠围墙(墙的长度不限),另三边用木栏围成,建成的苗圃为如图所示的长方形ABCD.已知木栏总长为120米,设AB边的长为x米,长方形ABCD的面积为S平方米.
(1)求S与x之间的函数关系式(不要求写出自变量x的取值范围).当x为何值时,S取得最值(请指出是最大值还是最小值)?并求出这个最值;
(2)学校计划将苗圃内药材种植区域设计为如图所示的两个相外切的等圆,其圆心分别为O1和O2,且O1到AB、BC、AD的距离与O2到CD、BC、AD的距离都相等,并要求在苗圃内药材种植区域外四周至少要留够0.5米宽的平直路面,以方便同学们参观学习.当(l)中S取得最值时,请问这个设计是否可行?若可行,求出圆的半径;若不可行,请说明理由.