设数列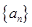 满足
满足
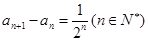
(1)求数列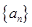 的通项公式;
的通项公式;
(2)令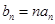 ,求数列
,求数列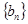 的前n项和
的前n项和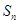
(本小题满分12分)已知函数f(x)=1+ (-2<x≤2).
(-2<x≤2).
(1)用分段的形式表示该函数;
(2)画出函数的图象.
(3)写出函数的值域、单调区间.
(本小题满分10分)已知全集U=R,集合A="{x|" log2(3-x)≤2},集合B={x|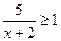 }
}
(1)求A,B(2)求( )∩B
)∩B
(本小题满分14分)已知函数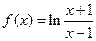
(Ⅰ)求函数的定义域,并证明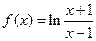 在定义域上是奇函数;
在定义域上是奇函数;
(Ⅱ)若
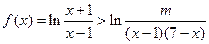 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)当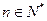 时,试比较
时,试比较 与
与 的大小关系.
的大小关系.
(本题14分)已知A、B分别是椭圆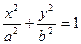 的左右两个焦点,O为坐标原点,点P
的左右两个焦点,O为坐标原点,点P  )在椭圆上,线段PB与y轴的交点M为线段PB的中点。
)在椭圆上,线段PB与y轴的交点M为线段PB的中点。
(1)求椭圆的标准方程;
(2)点 是椭圆上异于长轴端点的任一点,对于△ABC,求
是椭圆上异于长轴端点的任一点,对于△ABC,求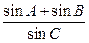 的值。
的值。
已知数列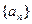 的前
的前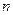 项和
项和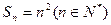 ,数列
,数列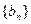 为等比数列,且满足
为等比数列,且满足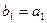 ,
,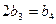
(1)求数列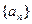 ,
,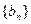 的通项公式;
的通项公式;
(2)求数列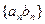 的前
的前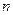 项和。
项和。