在 中,
中, ,点P从点A开始沿AB边向点B以
,点P从点A开始沿AB边向点B以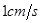 的速度移动,点Q从点B沿BC向点C以
的速度移动,点Q从点B沿BC向点C以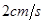 的速度移动.如果点P、Q分别从A、B同时出发.
的速度移动.如果点P、Q分别从A、B同时出发.
(1)几秒后, 的面积等于
的面积等于 ;
;
(2)经过几秒后,PQ之间的距离为 ;
;
(3)在P、Q两点的运动过程中, 可能是等腰三角形吗?请说明理由.
可能是等腰三角形吗?请说明理由.
球的体积计算公式为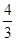 πR3,求半径为3.5cm的球的体积.(π取3.14,结果保留五个有效数字)
πR3,求半径为3.5cm的球的体积.(π取3.14,结果保留五个有效数字)
下列问题中,哪些是近似数?哪些是精确数?
(1)地球半径是6371米;
(2)一星期有7天;
(3)光的速度是每秒30万千米;
(4)我国古代的4大发明;
(5)某学校有36个班级;
(6)小明的体重是46.3公斤.
用四舍五入法,按括号中的要求对下列各数取近似值.
(1)349995(精确到百位);(2)349995(精确到千位)
(3)3.4995(精确到0.01);(4)0.003584(精确到千分位)
在一次立定跳远测验中,10名同学的成绩分别是(单位:米):1.63,1.85,1.64,1.71,1.53,1.64,1.38,1.66,1.75,1.81
(1)求他们的平均成绩;
(2)把平均成绩精确到0.1是多少?
(3)把平均成绩保留3个有效数字是多少?
要把一根长2.3米的圆钢锯成每段长16.5厘米的一段一段加工零件,一共可以锯出几段?