定义在 上的函数
上的函数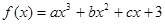 同时满足以下条件:
同时满足以下条件:
①  在
在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数;
②  是偶函数;
是偶函数;
③  在
在 处的切线与直线
处的切线与直线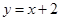 垂直.
垂直.
(I)求函数 的解析式;
的解析式;
(II)设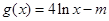 ,若存在
,若存在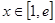 ,使
,使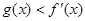 ,求实数
,求实数 的取值范围.
的取值范围.
(满分13分)如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,

求证:(1)FD∥平面ABC;
(2)AF⊥平面EDB.
(满分12分)
(1)已知△ABC三个顶点的坐标分别为A(4,1),B(0,3),C(2,4),边AC的中点为D,求AC边上中线BD所在的直线方程并化为一般式;
(2)已知圆C的圆心是直线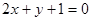 和
和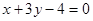 的交点上且与直线
的交点上且与直线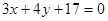 相切,求圆C的方程.
相切,求圆C的方程.
(本小题满分13分)已知椭圆的焦点在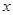 轴上,它的一个顶点恰好是抛物线
轴上,它的一个顶点恰好是抛物线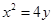 的焦点,离心率
的焦点,离心率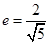 .
.
(1)求椭圆的标准方程;
(2)过椭圆的右焦点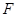 作与坐标轴不垂直的直线
作与坐标轴不垂直的直线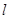 ,交椭圆于
,交椭圆于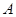 、
、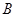 两点,设点
两点,设点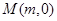 是线段
是线段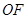 上的一个动点,且
上的一个动点,且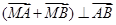 ,求
,求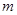 的取值范围;
的取值范围;
(3)设点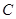 是点
是点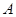 关于
关于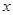 轴的对称点,在
轴的对称点,在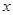 轴上是否存在一个定点
轴上是否存在一个定点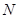 ,使得
,使得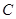 、
、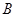 、
、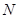 三点共线?若存
三点共线?若存
在,求出定点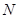 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(本小题满分13分)函数 (
(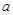 为常数)的图象过点
为常数)的图象过点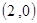 .
.
(1)求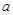 的值;
的值;
(2)函数 在区间
在区间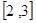 上有意义,求实数
上有意义,求实数 的取值范围;
的取值范围;
(3)讨论关于 的方程
的方程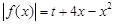 (
(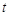 为常数)的正根的个数.
为常数)的正根的个数.
(本小题满分12分)正四棱柱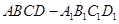 中,
中,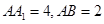 ,点
,点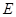 在
在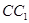 上,且
上,且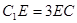 .
.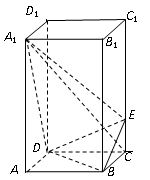
(1)证明: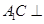 平面
平面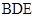 ;
;
(2)求二面角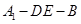 的余弦值.
的余弦值.