一只船在静水中的速度为4m/s,它要以最短时间渡过一条40 m宽、水流速度为3 m/s的河.求:
(1)船过河的时间;
(2)船过河的位移大小.
有一玻璃半球,右侧面镀银,光源S在其对称轴PO上(O为球心),且PO水平,如图所示.从光源S发出的一束细光射到半球面上,其中一部分光经球面反射后恰能竖直向上传播,另一部分光经过折射进入玻璃半球内,经右侧镀银面反射恰能沿原路返回.若球面半径为R,玻璃折射率为 ,求光源S与球心O之间的距离为多大?
,求光源S与球心O之间的距离为多大?
如图所示,在xOy平面内y>0的区域内分布着沿y轴负方向的匀强电场,在x轴下方有一边界平行的条形匀强磁场区域,匀强磁场的磁感应强度大小为B,方向垂直于xOy平面向外,磁场区域的上边界与x轴重合。质量为m、电荷量为q的带正电的粒子从y轴上的P点以初速度v0沿x轴正向射出,然后从x轴上的Q点射入磁场区域。已知OP=h,OQ= ,粒子的重力忽略不计。求:
,粒子的重力忽略不计。求: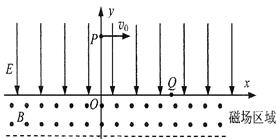
(1)粒子从x轴上的Q点射入磁场区域时的速度大小v ;
(2)若粒子未从磁场区域的下边界穿出,求条形磁场区域的最小宽度d0 ;
(3)若粒子恰好没从磁场区域的下边界穿出,求粒子从P点射入电场区域到经过磁场区域后返回x轴的时间t。
如图所示,滑板运动员从倾角为53°的斜坡顶端滑下,滑下的过程中他突然发现在斜面底端有一个高h="1.4" m、宽L="1.2" m的长方体障碍物,为了不触及这个障碍物,他必须在距水平地面高度H="3.2" m的A点沿水平方向跳起离开斜面(竖直方向的速度变为0)。已知运动员的滑板与斜面间的动摩擦因数μ=0.1,忽略空气阻力,重力加速度g取10m/s2。(已知sin53°=0.8,cos53°=0.6)求:
(1)运动员在斜面上滑行的加速度的大小;
(2)若运动员不触及障碍物,他从斜面上起跳后到落至水平面的过程所经历的时间;
(3)运动员为了不触及障碍物,他从A点沿水平方向起跳的最小速度。
在坐标系的第一象限内有一横截面为四分之一圆周的柱状玻璃体如图放置,其半径为R,圆心在O点,一光源发出的单色光始终垂直y轴射入玻璃体,已知玻璃体的折射率n= ,该光源从P点(四分之一圆周的柱状玻璃体的最高点)自由下落,当单色光源在R>y>0范围内运动时,求:
,该光源从P点(四分之一圆周的柱状玻璃体的最高点)自由下落,当单色光源在R>y>0范围内运动时,求:
①经过多长时间单色光可从圆弧面射出?
②在x轴上玻璃体的外部,单色光不能照射的长度(不考虑光沿x轴方向射入和经玻璃体全反射后的情况)。
如图所示,在xOy直角坐标系中,第Ⅰ象限内分布着方向垂直纸面向里的匀强磁场,第Ⅱ象限内分布着方向沿y轴负方向的匀强电场.初速度为零、带电荷量为q、质量为m的粒子经过电压为U的电场加速后,从x轴上的A点垂直x轴进入磁场区域,经磁场偏转后过y轴上的P点且垂直y轴进入电场区域,在电场中偏转并击中x轴上的C点.已知OA=OC=d. (粒子的重力不计).求
(1)离子进入磁场时的速度大小;
(2)电场强度E和磁感应强度B的大小.