某校为了解九年级男生1000米长跑的成绩，从中随机抽取了50-优题课

某校为了解九年级男生1000米长跑的成绩，从中随机抽取了50名男生进行测试，根据测试评分标准，将他们的得分进行统计后分为A、B、C、D四等，并绘制成下面的频数分布表和扇形统计图.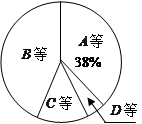

等第	成绩（得分）	频数（人数）	频率
A	10分	7	0.14
9分	x	m
B	8分	15	0.30
7分	8	0.16
C	6分	4	0.08
5分	y	n
D	5分以下	3	0.06
合计		50	1.00

（1）试直接写出x、y、m、n的值；
（2）求表示得分为C等的扇形的圆心角的度数；
（3）如果该校九年级共有男生200名，试估计这200名男生中成绩达到A等和B等的人数共有多少人？

科目数学题型解答题难度较易

知识点：统计量的选择

甲、乙、丙三位运动员在相同条件下各射靶10次，每次射靶的成绩如下：

甲：9，10，8，5，7，8，10，8，8，7

乙：5，7，8，7，8，9，7，9，10，10

丙：7，6，8，5，4，7，6，3，9，5

（1）根据以上数据完成下表：

	平均数	中位数	方差
甲	8	8
乙	8	8	2.2
丙	6		3

（2）根据表中数据分析，哪位运动员的成绩最稳定，并简要说明理由；

（3）比赛时三人依次出场，顺序由抽签方式决定，求甲、乙相邻出场的概率．

如图，在四边形 $ABCD$ 中， $AD = BC$ ， $∠ B = ∠ D$ ， $AD$ 不平行于 $BC$ ，过点 $C$ 作 $CE / / AD$ 交 $ΔABC$ 的外接圆 $O$ 于点 $E$ ，连接 $AE$ ．

（1）求证：四边形 $AECD$ 为平行四边形；

（2）连接 $CO$ ，求证： $CO$ 平分 $∠ BCE$ ．

[阅读理解]

我们知道， $1 + 2 + 3 + \dots + n = \frac{n (n + 1)}{2}$ ，那么 $1^{2} + 2^{2} + 3^{2} + \dots + n^{2}$ 结果等于多少呢？

在图1所示三角形数阵中，第1行圆圈中的数为1，即 $1^{2}$ ，第2行两个圆圈中数的和为 $2 + 2$ ，即 $2^{2}$ ， $\dots$ ；第 $n$ 行 $n$ 个圆圈中数的和为 $\underset{n 个 n}{\underset{︸}{n + n + \dots + n}}$ ，即 $n^{2}$ ，这样，该三角形数阵中共有 $\frac{n (n + 1)}{2}$ 个圆圈，所有圆圈中数的和为 $1^{2} + 2^{2} + 3^{2} + \dots + n^{2}$ ．

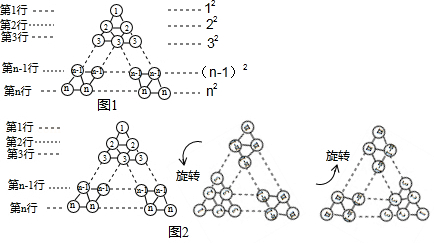
[规律探究]

将三角形数阵经两次旋转可得如图2所示的三角形数阵，观察这三个三角形数阵各行同一位置圆圈中的数（如第 $n - 1$ 行的第一个圆圈中的数分别为 $n - 1$ ，2， $n)$ ，发现每个位置上三个圆圈中数的和均为　　，由此可得，这三个三角形数阵所有圆圈中数的总和为： $3 (1^{2} + 2^{2} + 3^{2} + \dots + n^{2}) =$ 　　，因此， $1^{2} + 2^{2} + 3^{2} + \dots + n^{2} =$ 　　．

[解决问题]

根据以上发现，计算： $\frac{1^{2} + 2^{2} + 3^{2} + \dots + 2017^{2}}{1 + 2 + 3 + \dots + 2017}$ 的结果为　　．

如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点 $ΔABC$ 和 $ΔDEF$ （顶点为网格线的交点），以及过格点的直线 $l$ ．

（1）将 $ΔABC$ 向右平移两个单位长度，再向下平移两个单位长度，画出平移后的三角形．

（2）画出 $ΔDEF$ 关于直线 $l$ 对称的三角形．

（3）填空： $∠ C + ∠ E =$ 　　．

如图，游客在点 $A$ 处坐缆车出发，沿 $A - B - D$ 的路线可至山顶 $D$ 处，假设 $AB$ 和 $BD$ 都是直线段，且 $AB = BD = 600 m$ ， $α = 75 °$ ， $β = 45 °$ ，求 $DE$ 的长．

（参考数据： $\sin 75 ° \approx 0.97$ ， $\cos 75 ° \approx 0.26$ ， $\sqrt{2} \approx 1.41)$