[阅读理解]
我们知道,,那么结果等于多少呢?
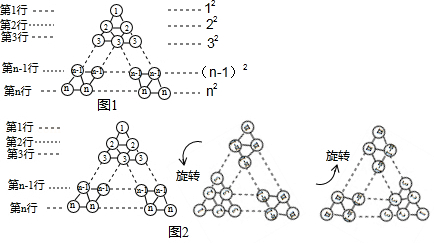
在图1所示三角形数阵中,第1行圆圈中的数为1,即,第2行两个圆圈中数的和为,即,;第行个圆圈中数的和为,即,这样,该三角形数阵中共有个圆圈,所有圆圈中数的和为.
[规律探究]
将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第行的第一个圆圈中的数分别为,2,,发现每个位置上三个圆圈中数的和均为 ,由此可得,这三个三角形数阵所有圆圈中数的总和为: ,因此, .
[解决问题]
根据以上发现,计算:的结果为 .
为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到 ;活动后,再次检查这部分学生的视力,结果如表所示.
|
分组 |
频数 |
|
|
2 |
|
|
3 |
|
|
5 |
|
|
8 |
|
|
17 |
|
|
5 |
(1)求所抽取的学生人数;
(2)若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.

请用学过的方法研究一类新函数 为常数, 的图象和性质.
(1)在给出的平面直角坐标系中画出函数 的图象;
(2)对于函数 ,当自变量 的值增大时,函数值 怎样变化?

保护视力要求人写字时眼睛和笔端的距离应超过 ,图1是一位同学的坐姿,把他的眼睛 ,肘关节 和笔端 的位置关系抽象成图2的 ,已知 , , ,他的这种坐姿符合保护视力的要求吗?请说明理由.(参考数据: , ,
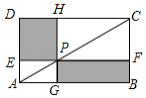
如图,点 在矩形 的对角线 上,且不与点 , 重合,过点 分别作边 , 的平行线,交两组对边于点 , 和 , .
(1)求证: ;
(2)证明四边形 和四边形 都是矩形,并直接写出它们面积之间的关系.
如图1,在直角坐标系 中,直线 交 轴, 轴于点 , ,点 的坐标是 ,过点 分别作 轴、 轴的垂线,垂足为 、 ,点 是线段 上的动点,以 为对称轴,作与 成轴对称的△ .
(1)当 时,求点 的坐标.
(2)当图1中的直线 经过点 ,且 时(如图 ,求点 由 到 的运动过程中,线段 扫过的图形与 重叠部分的面积.
(3)当图1中的直线 经过点 , 时(如图 ,以 为对称轴,作与 成轴对称的△ ,连接 , ,问是否存在点 ,使得△ 与△ 相似?若存在,求出 、 的值;若不存在,请说明理由.
