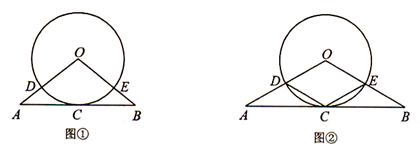为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到 ;活动后,再次检查这部分学生的视力,结果如表所示.
分组 |
频数 |
|
2 |
|
3 |
|
5 |
|
8 |
|
17 |
|
5 |
(1)求所抽取的学生人数;
(2)若视力达到4.8及以上为达标,估计活动前该校学生的视力达标率;
(3)请选择适当的统计量,从两个不同的角度分析活动前后相关数据,并评价视力保健活动的效果.

(本题12分) 如图,已知二次函数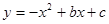 的图象与
的图象与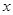 轴交于点
轴交于点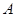 、
、 ,与
,与 轴交于点
轴交于点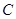 ,其顶点为
,其顶点为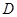 ,且直线
,且直线 的解析式为
的解析式为 .
.(1) 求二次函数的解析式.
(2) 求△ABC外接圆的半径及外心的坐标;
(3) 若点P是第一象限内抛物线上一动点,求四边形ACPB的面积最大值.

(本题12分) 在正方形网格中,A、B为格点,以点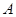 为圆心,
为圆心,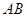 为半径作圆
为半径作圆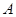 交网格线于点
交网格线于点 (如图(1)),过点
(如图(1)),过点 作圆的切线交网格线于点
作圆的切线交网格线于点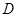 ,以点
,以点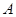 为圆心,
为圆心,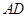 为半径作圆交网格线于点
为半径作圆交网格线于点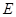 (如图(2)).
(如图(2)).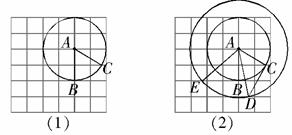
问题:(1) 求
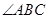 的度数;
的度数;(2) 求证:
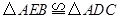 ;
;(3)
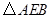 可以看作是由
可以看作是由 经过怎样的变换得到的?并判断
经过怎样的变换得到的?并判断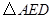 的形状(不用说明理由).
的形状(不用说明理由).(4) 如图(3),已知直线
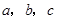 ,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形
,且a∥b,b∥c,在图中用直尺、三角板、圆规画等边三角形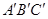 ,使三个顶点
,使三个顶点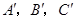 ,分别在直线
,分别在直线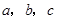 上.要求写出简要的画图过程,不需要说明理由.
上.要求写出简要的画图过程,不需要说明理由.
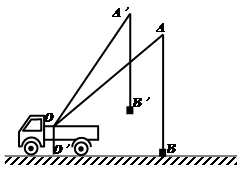
.(本题10分) 小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不
变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊缆A′B′=AB.且cosA=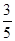 ,sinA′=
,sinA′=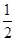 .
.(1) 求此重物在水平方向移动的距离及在竖直方向移动的距离;
(2) 若这台吊车工作时吊杆最大水平旋转角度为120°,吊杆与水平线的倾角可以从30°转到60°,求吊车工作时,工作人员不能站立的区域的面积。
(本题8分) 时代广场一个销售点在销售“盼盼”牌某款童装时,平均每天可售出20件,每件盈利40元,为扩大销售,增加盈利,服装销售点老板打算在“春节”期间采取“购买童装送玩具”活动,并购进了一批样式多样,成本均为4元的玩具。市场调研表明,如果每买1件童装赠送1个玩具,那么平均每天就能多售出8件.(1) 老板要想使这项“购买童装送玩具”活动的利润平均每天达到1200元,买每件童装应送多少个玩具?
(2) 若利润平均每天要超过1200元,买每件童装应送多少个玩具?(直接回答一个结论即可)
(本题10分)已知,如图,△OAB中,OA=OB,⊙O经过AB的中点C,且与OA、OB分别交于点D、E. (1) 如图①,判断直线AB与⊙O的位置关系并说明理由;
(2) 如图②,连接CD、CE,当△OAB满足什么条件时,四边形ODCE为菱形,并证明你的结论。