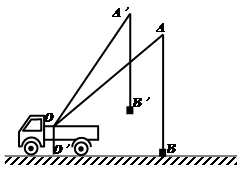
.(本题10分) 小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高OO′=2米.当吊臂顶端由A点抬升至A′点(吊臂长度不
变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊缆A′B′=AB.且cosA=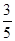 ,sinA′=
,sinA′=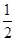 .
.(1) 求此重物在水平方向移动的距离及在竖直方向移动的距离;
(2) 若这台吊车工作时吊杆最大水平旋转角度为120°,吊杆与水平线的倾角可以从30°转到60°,求吊车工作时,工作人员不能站立的区域的面积。
(本题8分)在平面直角坐标系中,顺次连接A(-2,1),B(-2,-1),C(2,-2),D(2,3) ,A(-2,1)各点,你会得到一个什么图形?试求出该图形的面积.
(本题6分)如图,已知∠1 =∠2,∠B =∠C,可推得AB∥CD。
理由如下:
∵∠1 =∠2(已知),
且∠1 =∠CGD(__________________________)
∴∠2 =∠CGD(等量代换)
∴CE∥BF(_______________________________)
∴∠=∠BFD(__________________________)
又∵∠B =∠C(已知)
∴∠BFD =∠B()
∴AB∥CD(________________________________)
(本题6分)如图:直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=67°,∠ACB=74°,
∠AED=48°,求∠BDF的度数。
如图,平面直角坐标系中,点B的坐标为(1,2),过点B作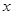 轴的垂线,垂足为A,连结OB,将△OAB沿OB折叠,使点A落在点A′处,A′B与
轴的垂线,垂足为A,连结OB,将△OAB沿OB折叠,使点A落在点A′处,A′B与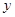 轴交于点F.
轴交于点F.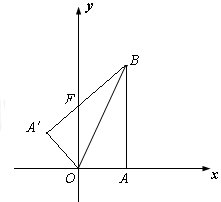
(1)求证:OF=BF;
(2)求BF的长;
(3)求过点A′的双曲线的解析式。
如图,一次函数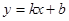 的图像与反比例函数
的图像与反比例函数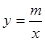 的图像交于
的图像交于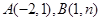 两点。
两点。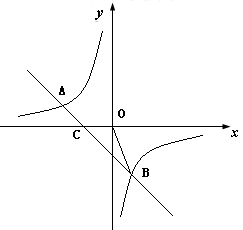
求:(1)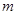 的值;
的值;
(2)求一次函数的解析式;
(3)若直线AB交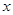 轴于点C,求△OBC的面积.
轴于点C,求△OBC的面积.