如图,△OAB的底边经过⊙O上的点C,且OA=OB,CA=CB,⊙O与OA、OB分别交于D、E两点.
(1)求证:AB是⊙O的切线;
(2)若D为OA的中点,阴影部分的面积为 ,求⊙O的半径r.
,求⊙O的半径r.
(1)先化简,再求值 ,其中
,其中 满足
满足 ;
;
(2)已知多项式 ,其中
,其中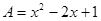 ,小马在计算
,小马在计算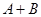 时,由于粗心把
时,由于粗心把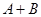 看成了
看成了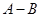 求得结果为
求得结果为 ,请你帮小马算出
,请你帮小马算出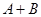 的正确结果。
的正确结果。
解方程:(1) ;(2)
;(2)
计算:(1)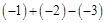 (2)
(2)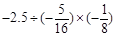
(3) (4)
(4)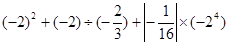
在△ABC中,AB=AC,D为BC边中点,以点D为顶点作∠MDN=∠B。
(1)当射线DN经过点A时,DM交AC边于点E,如图(1),不添加辅助线,直接写出图中所有与△ADE相似的三角形(不需要证明);
(2)将∠MDN绕点D沿逆时针方向旋转,DM、DN分别交线段AC、AB于点E、F(点E与点A不重合,如图(2))。
①求证:△BDF~△CED;②△BDF与△DEF是否相似?并证明你的结论。
某文具店老板第一次用1600元购进一批某种品牌文具,很快销售完毕;第二次购进该种品牌文具时,发现每件文具的进价比第一次上涨了2元。老板用2700元购进了第二批该种品牌的文具,所购进文具的数量是第一次购进数量的1.5倍,同样很快销售完毕。两批文具的售价均为每件22元。
(1)问第二次购进了多少件该种品牌的文具?
(2)文具店老板在这两笔生意中共盈利多少元?