如图，已知抛物线y＝
x2＋bx＋c与坐标轴交于A、B、C三点， A点的坐标为（－1，0），过点C的直线y＝
x－3与x轴交于点Q，点P是线段BC上的一个动点，过P作PH⊥OB于点H．若PB＝5t，且0＜t＜1．
（1）填空：点C的坐标是 ，b＝ ，c＝ ；
（2）求线段QH的长（用含t的式子表示）；
（3）依点P的变化，是否存在t的值，使以P、H、Q为顶点的三角形与△COQ相似？若存在，求出所有t的值；若不存在，说明理由．
本市出租车的收费标准为：3千米以内（含3千米）收费5元，超过3千米的部分每千米收费1．20元（不足1千米按1千米计算），另加收0．60元的返空费．
（1）设行驶路程为x千米（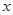
≥3且取整数），用x表示出应收费y元的代数式；
（2）当收费为10．40元时，该车行驶路程不超过多少千米？路程数在哪个范围内？
某公园欲建如图13-2-3所示形状的草坪（阴影部分），求需要铺设草坪多少平方米？若每平方米草坪需120元，则为修建该草坪需投资多少元？（单位：米）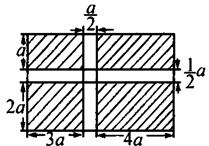
求下列分式的值：
（1）
其中a＝3．
（2）
其中x＝2，y＝－1．
x为何值时，分式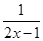
与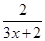
的值相等？并求出此时分式的值．
（1）已知分式
，x取什么值时，分式的值为零？
（2）x为何值时，分式
的值为正数？