计算:
(1) ;(2)
;(2)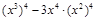 ;(3)
;(3) .
.
已知:如图,△ABC中,点D、E分别为BC、AC边中点,连接AD,连接DE,过A点作AF∥BC,交DE的延长线于F.连接CF,
(1)求证:四边形ADCF是平行四边形;
(2)对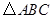 添加一个条件,使得四边形ADCF是矩形,并进行证明;
添加一个条件,使得四边形ADCF是矩形,并进行证明;
(3)在(2)的基础上对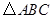 再添加一个条件,使得四边形ADCF是正方形,不必证明.
再添加一个条件,使得四边形ADCF是正方形,不必证明.
如图,已知B港口位于A观测点北偏东53.2°方向,且其到A观测点正北方向的距离BD的长为16海里,一艘货轮从B港口以40海里/h的速度沿∠ABC=45°的BC方向航行.现测得C处位于A观测点北偏东79.8°(即∠DAC=79.8°)方向.求此时货轮C与AB之间的最近距离(精确到0.1海里).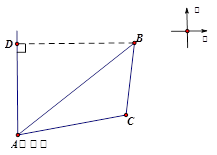
(参考数据:sin53.2°≈0.80,cos53.2°≈0.60,sin79.8°≈0.98,cos79.8°≈0.18,tan26.6°≈0.50,)
我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x (小时)变化的函数图象,其中BC段是双曲线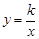 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题: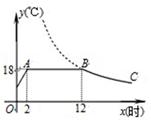
(1)恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
小明和小亮用如下的同一个转盘进行“配紫色”游戏.游戏规则如下:连续转动两次转盘,如果两次转盘转出的颜色相同或配成紫色(若其中一次转盘转出蓝色,另一次转出红色,则可配成紫色),则小明得1分,否则小亮得1分.你认为这个游戏对双方是否公平?请说明理由.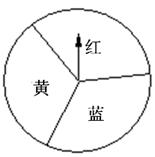
如图,将一付三角板拼成如图所示的图形,过点C作CF平分∠DCE交DE于点F.
(1)求证:CF∥AB;
(2)求∠DFC的度数.