从甲地到乙地有A1、A2两条路线，从乙地到丙地有B1、B2、B3三条路线，其中A1B2是从甲地到丙地的最短路线．一个人任意选了一条从甲地到丙地的路线，他恰好选到最短路线的概率是多少？
如图，AB＝AC，AB为⊙O的直径，AC、BC分别交⊙O于E、D，连结ED、BE．
（1）试判断DE与BD是否相等，并说明理由；
（2）如果BC＝6，AB＝5，求BE的长．
已知抛物线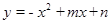
经过点A （1，0）, B（6，0）.
（1）求抛物线的解析式；
（2）当y＜0,直接写出自变量x的取值范围．
（3）抛物线与y轴交于点D， P是x轴上一点，且△PAD是以AD为腰的等腰三角形，试求P点坐标。
.如图，有长为30m的篱笆，一面利用墙（墙的最大可用长度为10m），围成中间隔有一道篱笆（平行于AB）的矩形花圃．设花圃的一边AB为xm，面积为ym2．
（1）求y与x的函数关系式；
（2）如果要围成面积为63m2的花圃，AB的长是多少？
（3）能围成比63m2更大的花圃吗？如果能，请求出最大面积；如果不能，请说明理由．
如图，AC，BD是⊙O的两条直径.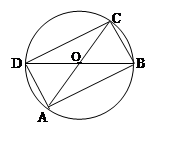
（1）判断四边形ABCD的形状，并说明理由.
（2）若⊙O的直径为8，∠AOB=120°，求四边形ABCD的周长和面积.
已知某二次函数当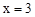
时，函数有最大值-1，且函数图像与y轴交于（0，-4），
求该二次函数的解析式.