已知A=x2-5x,B=x2-10x+5,求A+2B的值.
化简并求值:9x+6x2-3(x- x2),其中x=-2
x2),其中x=-2
化简下列各式
⑴ 2(3a-5)+5
⑵ -2x-(3x-1)
如图,抛物线y= x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).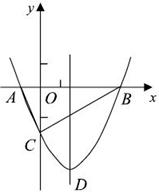
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
已知:□ABCD的两边AB,AD的长是关于x的方程 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么□ABCD的周长是多少?