（1）如图①，P为△ABC的边AB上一点（P不与点A、点B重合），连接PC，如果△CBP∽△ABC，那么就称P为△ABC的边AB上的相似点．
画法初探
①如图②，在△ABC中，∠ACB＞90°，画出△ABC的边AB上的相似点P（画图工具不限，保留画图痕迹或有必要的说明）；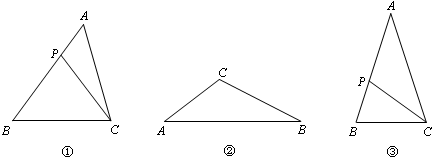
辩证思考
②是不是所有的三角形都存在它的边上的相似点？如果是，请说明理由；如果不是，请找出一个不存在边上相似点的三角形；
特例分析
③已知P为△ABC的边AB上的相似点，连接PC，若△ACP∽△ABC，则△ABC的形状是 ；
④如图③，在△ABC中，AB＝AC，∠A＝36°，P是边AB上的相似点，求的值．
（2）在矩形ABCD中，AB＝a，BC＝b（a≥b）．P是AB上的点（P不与点A、点B重合），作PQ⊥CD，垂足为Q．如果矩形ADQP∽矩形ABCD，那么就称PQ为矩形ABCD的边AB、CD上的相似线．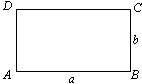
①类比（1）中的“画法初探”，可以提出问题：对于如图④的矩形ABCD，在不限制画图工具的前提下，如何画出它的边AB、CD上的相似线PQ呢？
你的解答是： （只需描述PQ的画法，不需在图上画出PQ）．
②请继续类比（1）中的“辩证思考”、“特例分析”两个栏目对矩形的相似线进行研究，要求每个栏目提出一个问题并解决．
已知抛物线y1=ax2+bx+c的顶点坐标为（
，
）且经过点A（1，0），直线y2=x+m恰好也经过点A
（1）分别求抛物线和直线的解析式；
（2）当x取何值时，函数值y2＞y1；
（3）当0≤x≤2时，直接写出y2和y1的最小值分别为多少？
在一个不透明的盒子里，装有四个分别标有数字1，2，3，4的小球，它们的形状、大小、质地等完全相同．小米先从盒子中随机取出一个小球，记下数字为x，且不放回盒子，再由小华随机取出一个小球，记下数字为y．
（1）用列表法或画树状图表示出（x，y）的所有可能出现的结果；
（2）求小米、小华各取一次小球所确定的点（x，y）落在反比例函数y=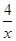
的图象上的概率．
判断下列二次函数的图象与x轴有无交点，若有请求出交点坐标；若无请说明理由．
（1）y=
-6x
（2）y=2x2-12x+18．
某商场销售甲、乙两种品牌的智能手机，这两种手机的进价和售价如下表所示：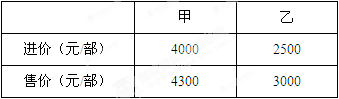
该商场计划购进两种手机若干部，共需15．5万元，预计全部销售后可获毛利润共2．1万元．
（毛利润=（售价﹣进价）×销售量）
（1）该商场计划购进甲、乙两种手机各多少部？
（2） 通过市场调研，该商场决定在原计划的基础上，减少甲种手机的购进数量，增加乙种手机的购进数量．已知乙种手机增加的数量是甲种手机减少的数量的2倍，而且用于购进这两种手机的总资金不超过16万元，该商场怎样进货，使全部销售后获得的毛利润最大？并求出最大毛利润．
如图，已知在等腰直角三角形△DBC中，∠BDC=90°，BF平分∠DBC，与CD相交于点F，延长BD到A，使DA=DF，
（1）试说明：△FBD≌△ACD；
（2）延长BF交AC于E，且BE⊥AC，试说明：CE＝