某商场销售甲、乙两种品牌的智能手机,这两种手机的进价和售价如下表所示: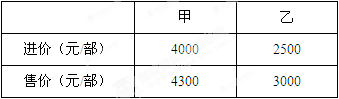
该商场计划购进两种手机若干部,共需15.5万元,预计全部销售后可获毛利润共2.1万元.
(毛利润=(售价﹣进价)×销售量)
(1)该商场计划购进甲、乙两种手机各多少部?
(2) 通过市场调研,该商场决定在原计划的基础上,减少甲种手机的购进数量,增加乙种手机的购进数量.已知乙种手机增加的数量是甲种手机减少的数量的2倍,而且用于购进这两种手机的总资金不超过16万元,该商场怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.