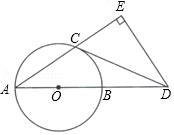
如图, 的直径为 ,点 在 上,点 , 分别在 , 的延长线上, ,垂足为 , .
(1)求证: 是 的切线;
(2)若 , ,求 的长.
已知:如图,AB是⊙O的直径,CD是⊙O的弦, 且AB⊥CD,垂足为E,联结OC, OC=5.
(1)若CD=8,求BE的长;
(2)若∠AOC=150°, 求扇形OAC的面积.
已知二次函数 .
.
(1)将 化成y ="a" (x - h) 2 + k的形式;
化成y ="a" (x - h) 2 + k的形式;
(2)指出该二次函数图象的对称轴和顶点坐标;
(3)当x取何值时,y随x的增大而增大?
已知:如图,在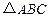 中,D是AC上一点,联结BD,且∠ABD =∠ACB.
中,D是AC上一点,联结BD,且∠ABD =∠ACB.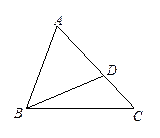
(1)求证:△ABD∽△ACB;
(2)若AD=5,AB= 7,求AC的长.
计算: 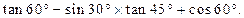
△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,把一个三角板的直角顶点放在点D处,将三角板绕点D旋转且使两条直角边分别交AB、AC于E、F .
(1)如图1,观察旋转过程,猜想线段AF与BE的数量关系并证明你的结论;
(2)如图2,若连接EF,试探索线段BE、EF、FC之间的数量关系,直接写出你的结论(不需证明);
(3)如图3,若将“AB=AC,点D是BC的中点”改为:“∠B=30°,AD⊥BC于点D”,其余条件不变,探索(1)中结论是否成立?若不成立,请探索关于AF、BE的比值.