已知二次函数 .
.
(1)将 化成y ="a" (x - h) 2 + k的形式;
化成y ="a" (x - h) 2 + k的形式;
(2)指出该二次函数图象的对称轴和顶点坐标;
(3)当x取何值时,y随x的增大而增大?
在平面直角坐标系xOy中,二次函数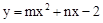 的图象过A(-1,-2)、B(1,0)两点.
的图象过A(-1,-2)、B(1,0)两点.
(1)求此二次函数的解析式并画出二次函数图象;
(2)点P(t,0)是x轴上的一个动点,过点P作x轴的垂线交直线AB于点M,交二次函数的图象于点N.当点M位于点N的上方时,直接写出t的取值范围.
一学校为了绿化校园环境,向某园林公司购买力一批树苗,园林公司规定:如果购买树苗不超过60棵,每棵售价120元;如果购买树苗超过60棵,每增加1棵,所出售的这批树苗每棵售价均降低0.5元,但每棵树苗最低售价不得少于100元,该校最终向园林公司支付树苗款8800元,请问该校共购买了多少棵树苗?
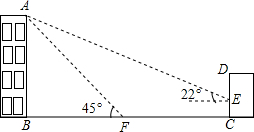
如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22º时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45º时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).求教学楼AB的高度.(参考数据:sin22º≈ ,cos22º≈
,cos22º≈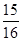 ,tan22º≈
,tan22º≈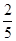 )
)
如图所示,在梯形ABCD中,AD∥BC,∠BDC=90°,E为DC上一点,∠BDE=∠DBC.
(1)求证:DE=CE;
(2)若 ,试判断四边形ABED的形状,并说明理由.
,试判断四边形ABED的形状,并说明理由.
某社区准备在甲、乙两位射箭爱好者中选出一人参加集训,两人各射了5箭,他们的总成绩(单位:环)相同,小宇根据他们的成绩计算了甲成绩的平均数和方差(见小宇的作业).

(1)求a和乙的方差S乙;
(2)请你从平均数和方差的角度分析,谁将被选中.