如图,在平面直角坐标系 中,A(1,2),B(3,1),C(-2,-1).
中,A(1,2),B(3,1),C(-2,-1).
(1)在图中作出 关于
关于 轴的对称图形
轴的对称图形 .
.
(2)写出点 的坐标(直接写答案).
的坐标(直接写答案).
A 1 ______________
B 1 ______________
C 1 ______________
我国自2011年9月1日起,个人工资、薪金所得税征收办法规定:月收入不超过3500元的部分不收税;月收入超过3500元的部分征收3%的所得税……如某人月收入超3860元,他应缴纳个人工资、薪金所得税为:
(3860-3500)×3%=10.8(元)
(1)当月收入超过3500元而又不超过5000元时,写出应缴纳个人工资、薪金所得税y(元)与月收入(x)之间的关系式;
(2)某人月收入为4160元,他应缴纳个人工资、薪金所得税多少元?
(3)如果某人本月缴纳个人工资、薪金所得税19.2元,那么此人本月工资、薪金收入是多少元?
某电信公司手机的A类收费标准如下:不管通话时间多长,每部手机每月必须交月租费12元,另外,通话费按0.2元/min计.
(1)写出每月应缴费用y(元)与通话时间x(min)之间的关系式;
(2)某手机用户这个月通话时间为180 min,他应缴费多少元?
(3)如果该手机用户本月预缴了100元的话费,那么该用户本月可通话多长时间?
中国人饮食中食盐的含量偏大.据研究每人每天的食盐摄入量以不超过6g为宜.为控制食盐摄入量,某市向每个家庭发放一个向盐勺(容量2g).设家庭人口数为x,家庭每天所应摄入盐的勺数的最大值为y.
(1)当x=3时,y的值是多少?
(2)写出x与y之间的关系式和x的取值范围.
已知等边三角形ABC的边长是6cm。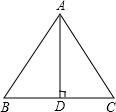
求:(1)高AD的长;
(2)△ABC的面积.
长方形ABCD的长与宽分别为6, 4,建立适当的坐标系,写出各个顶点的坐标.