某电信公司手机的A类收费标准如下：不管通话时间多长，每部手机每月必须交月租费12元，另外，通话费按0.2元/min计.
（1）写出每月应缴费用y（元）与通话时间x（min）之间的关系式；
（2）某手机用户这个月通话时间为180 min，他应缴费多少元？
（3）如果该手机用户本月预缴了100元的话费，那么该用户本月可通话多长时间？
问题：一架电梯的最大载重是1000千克，现有13位“重量级”的乘客要搭乘电梯，已知其中11位先生的平均体重是80千克，2位女士的平均体重是70千克，请问他们能否一起安全地搭乘这架电梯？他们的平均体重是多少千克？
小飞的解答：11位先生的总体重=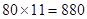
（千克）
2位女士的总体重=70×2=140（千克）
13位乘客的总体重=880+140=1020（千克）
因为总体重超过了电梯的最大载重，所以他们不能一起安全地搭乘.
平均体重是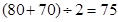
（千克）
你怎样评价小飞的解答？只有在什么情况下才可以采取这种策略求平均数？
甲、乙两人两次同时在同一粮站购买粮食（假设两次购买粮食的单价不同），甲每次购买粮食100千克，乙每次购买粮食用去100元，设甲、乙两人第一次购买粮食的单价为每千克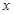
元，第二次购买粮食的单价为每千克
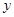元.
（1）用含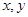
的代数式表示甲两次购买粮食共要付款，乙两次共购买千克粮食，若甲两次购粮的平均单价为每千克
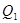元，乙两次购粮的平均单价为每千克
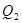元，则=，=.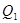
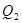（2）若规定两次购粮的平均单价低者，购粮方式是合算的，请你判断甲、乙两人购粮方式哪一个更合算些，并说明理由.
某同学在这学期的前四次的数学测试中，得分依次为：95，82，76和88，马上要进行第五次数学测试了，她希望五次成绩的平均数能够达到或超过85分，那么，这次测试她至少要考多少分？
为了了解用电量的大小，某家庭在6月初连续几天观察电表的度数，显示如下表：
请你估计这个家庭六月份的总用电量是多少度？
有位学生在一次考试中的得分分别是：18，73，78，90，100，考分为73的同学是在平均分之上还是之下？你认为他在5人中考分属“中上”水平吗？