△ABC中,∠BAC=90°,AB=AC,点D是BC的中点,把一个三角板的直角顶点放在点D处,将三角板绕点D旋转且使两条直角边分别交AB、AC于E、F .
(1)如图1,观察旋转过程,猜想线段AF与BE的数量关系并证明你的结论;
(2)如图2,若连接EF,试探索线段BE、EF、FC之间的数量关系,直接写出你的结论(不需证明);
(3)如图3,若将“AB=AC,点D是BC的中点”改为:“∠B=30°,AD⊥BC于点D”,其余条件不变,探索(1)中结论是否成立?若不成立,请探索关于AF、BE的比值.
生活中,在分析研究比赛成绩时经常要考虑不等关系.例如:一射击运动员在一次比赛中将进行10次射击,已知前7次射击共中61环,如果他要打破88环(每次射击以1到10的整数环计数)的记录,问第8次射击不能少于多少环?
我们可以按以下思路分析:
首先根据最后二次射击的总成绩可能出现的情况,来确定要打破88环的记录,第8次射击需要得到的成绩,并完成下表:
最后二次射击总成 绩 绩 |
第8次射击需得成绩 |
| 20环 |
|
| 19环 |
|
| 18环 |
根据以上分析可得如下解答:
解:设第8次射击的成绩为x环,则可列出一个关于x的不等式:()解得()
所以第8次设计不能少于 ( )环
为了解我市3路公共汽车的运营情况,公交部门随机统计了某天3路公共汽车每个运行班次的载客量,得到如下频数分布直方图.如果以各组的组中值代表各组实际数据,请分析统计数据完成下列问题.
(1)找出这天载客量的中位数,说明这个中位数的意义;
(2)估计3路公共汽车平均每班的载客量大约是多少?
(3)计算这天载客量在平均载客量以上班次占总班次的百分数.
(注:一个小组的组中值是指这个小组的两个端点数的平均数)
在同一 直角坐标系中反比例函数
直角坐标系中反比例函数 的图象与一次函数y=kx+b的图象相交,且其中一个交点A的坐标为(﹣2,3),若一次函数的图象又与x轴相交于点
的图象与一次函数y=kx+b的图象相交,且其中一个交点A的坐标为(﹣2,3),若一次函数的图象又与x轴相交于点 B,且△AOB的面积为6(点O为坐标原点).求一次函数与反比例函数的解析式.
B,且△AOB的面积为6(点O为坐标原点).求一次函数与反比例函数的解析式.
如图所示,四边形ABCD是正方形,点E是边BC 的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG.
的中点且∠AEF=90°,EF交正方形外角平分线CF于点F,取边AB的中点G,连接EG.
(1)求证:EG=CF;
(2)将△ECF绕点E逆时针旋转90°,请在图中直接画出旋转后的图形,并指出旋转后CF与EG的位置关系.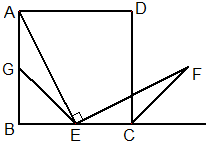
解方程组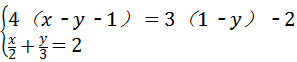 .
.