碰撞的恢复系数的定义为
=
，其中
和
分别是碰撞前两物体的速度，
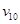和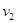
分别是碰撞后两物体的速度。弹性碰撞的恢复系数=1，非弹性碰撞的＜1,某同学借用验证动量守恒定律的实验装置（如图所示）物质弹性碰撞的恢复系数是否为1，实验中使用半径相等的钢质小球1和2（它们之间的碰撞可近似视为弹性碰撞），且小球1的质量大于小球2的质量。实验步骤如下安装好实验装置，做好测量前的准备，并记下重垂线所指的位置O。
第一步，不放小球2，让小球1从斜槽上A点由静止滚下，并落在地面上。重复多次，用尽可能小的圆把小球的所有落点圈在里面，其圆心就是小球落点的平均位置。
第二步，把小球2放在斜槽前端边缘处的C点，让小球1从A点由静止滚下，使它们碰撞。重复多次，并使用与第一步同样的方法分别标出碰撞后两小球落点的平均位置。
第三步，用刻度尺分别测量三个落地点的平均位置离O点的距离，即线段OM、OP、ON的长度。在上述实验中，
（1）P点是 的平均位置，M点是 的平均位置，N点是 的平均位置。
（2）请写出本实验的原理 写出用测量的量表示的恢复系数的表达式
（3）三个落地点距O点的距离OM、OP、ON与实验所用的小球质量是否有关？
某同学通过设计实验探究绕轴转动而具有的动能与哪些因素有关。他以圆形砂轮为研究对象，研究其转动动能与质量、半径、角速度的具体关系。砂轮由动力带动匀速旋转测得其角速度ω，然后让砂轮脱离动力，用一把弹性尺子与砂轮接触使砂轮慢慢停下，设尺子与砂轮间的摩擦力大小恒为10/π牛（不计转轴与砂轮的摩擦），分别取不同质量、不同半径的砂轮，使其以不同的角速度旋转进行实验，得到数据如下表所示：
（1）由上述数据推导出转动动能Ek与质量m、角速度ω、半径r的关系式 为(比例系数用k表示）。合理猜想K的值为单位（填“有”或“没有”）
（2）以上实验运用了物理学中的一个重要的实验方法是。
| 半径r/cm |
质量m/kg |
角速度ω(rad/s) |
转动动能Ek/J |
| 4 |
1 |
2 |
6.4 |
| 4 |
1 |
3 |
14.4 |
| 4 |
1 |
4 |
25.6 |
| 4 |
2 |
2 |
12.8 |
| 4 |
3 |
2 |
19．2 |
| 4 |
4 |
2 |
25.6 |
| 8 |
1 |
2 |
25.6 |
| 12 |
1 |
2 |
57.6 |
| 16 |
1 |
2 |
102．4 |
某同学为了测定一根轻弹簧压缩到最短时具有的弹性势能的大小，将弹簧的一端固定在光滑水平桌面上，如图所示，用已知质量为m的钢球将弹簧压缩至最短，而后突然释放，弹簧的弹性势能转化为钢球的动能，钢球将沿水平方向飞出桌面，实验时:
（1）还需要测定的物理量及物理量的符号是, ；
（2）计算弹簧最短时弹性势能的关系式是
＝。
探究加速度与力的关系装置如图所示。带滑轮的长木板水平放置，细绳通过两光滑滑轮分别与弹簧秤挂钩和沙桶连接，细线与桌面平行．将木块放在靠近打点计时器的一端，缓慢向沙桶中添加细沙，直到木块开始运动，记下木块运动后弹簧秤的示数F，通过纸带求出木块运动的加速度a。将木块放回原处，向沙桶中添加适量细沙，释放木块……，如此重复，获取多组a、F数据。
（1）关于该实验的操作，以下说法正确的是
| A．实验过程中，应先闭合打点计时器开关，再释放小车 |
| B．通过缓慢添加细沙，可以方便地获取多组实验数据 |
| C．每次添加细沙后，需测出沙及沙桶的质量 |
| D．实验过程要确保沙及沙桶的质量远小于木块的质量 |
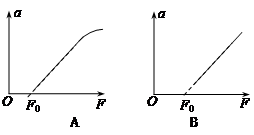
（2）某同学根据实验数据做出了两个a-F图象如图所示，正确的是；已知图线与横轴的交点为F0，则木块所受的滑动摩擦力大小为。
用图甲所示的装置来研究自由落体运动，得到的一条纸带如图图乙所示，O为打下的第一个点，相邻两计数点间的时间间隔为0.1s。测得O点到各计数点间的距离为：hOA=48.5mm，hOB=193.9mm，hOC=436.5mm，hOD=776.0mm.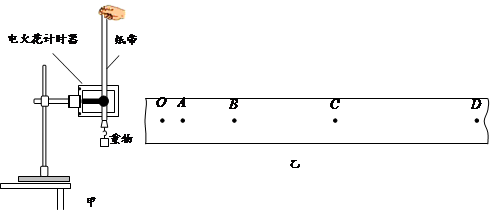
（1）计时器打C点时重物下落的速度vC=m/s（保留三位有效数字）；
（2）重物自由下落的加速度g测=m/s2（保留三位有效数字）。
（3）某同学想利用测得的vC、g测的值，以及O、C间的距离h，判断g测h与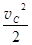
是否相等，来验证机械能是否守恒。你认为此方案是否可行？。（选填“是”或“否”）
某同学做测定弹簧劲度系数的实验。他测出了弹簧长度l与对应弹力F的五组数据后，在F-l坐标系中描出了对应的五个点，如图所示。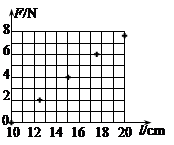
（1）在图中绘出F-l图线；
（2）由图线求得弹簧的劲度系数k=N/m.（保留两位有效数字）。