某中学号召本校学生在本学期参加市创办卫生城的相关活动,学校团委对该校学生是否关心创卫活动用简单抽样方法调查了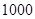 位学生(关心与不关心的各一半),
位学生(关心与不关心的各一半),
结果用二维等高条形图表示,如图.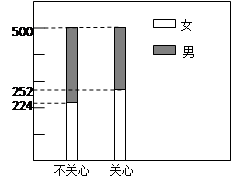
(1)完成列联表,并判断能否有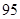 ℅的把握认为是否关心创卫活动与性别有关?
℅的把握认为是否关心创卫活动与性别有关?
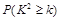 |
0.10 |
0.05 |
0.01 |
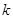 |
2.706 |
3.841 |
6.635 |
(参考数据与公式:
 ;
;
| |
女 |
男 |
合计 |
| 关心 |
|
|
500 |
| 不关心 |
|
|
500 |
| 合计 |
|
524 |
1000 |
(2)已知校团委有青年志愿者100名,他们已参加活动的情况记录如下:
| 参加活动次数 |
1 |
2 |
3 |
| 人数 |
10 |
50 |
40 |
(i)从志愿者中任选两名学生,求他们参加活动次数恰好相等的概率;
(ii)从志愿者中任选两名学生,用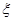 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量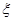 的分布列及数学期望
的分布列及数学期望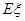 .
.
(本小题满分13分)设函数 ,
,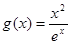 .已知曲线
.已知曲线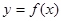 在点
在点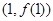 处的切线与直线
处的切线与直线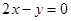 平行.
平行.
(Ⅰ)求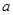 的值;
的值;
(Ⅱ)是否存在自然数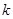 ,使得方程
,使得方程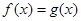 在
在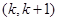 内存在唯一的根?如果存在,求出
内存在唯一的根?如果存在,求出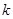 ;如果不存在,请说明理由;
;如果不存在,请说明理由;
(Ⅲ)设函数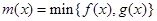 (
(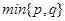 表示,
表示,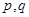 中的较小值),求
中的较小值),求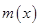 的最大值.
的最大值.
(本小题满分12分)已知函数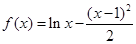 .
.
(Ⅰ)求函数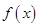 的单调递增区间;
的单调递增区间;
(Ⅱ)证明:当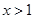 时,
时, .
.
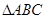 中,
中,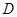 是
是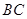 上的点,
上的点,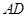 平分
平分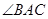 ,
,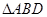 面积是
面积是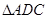 面积的2倍.
面积的2倍.
(Ⅰ) 求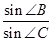 ;
;
(Ⅱ)若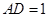 ,
,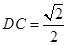 ,求
,求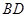 和
和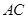 的长.
的长.
(本小题12分)已知向量 ,
, ,函数
,函数
(Ⅰ)求函数 的单调递增区间;
的单调递增区间;
(Ⅱ)在 中,内角
中,内角 的对边分别为
的对边分别为 ,且
,且 ,若对任意满足条件的
,若对任意满足条件的 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分11分)已知数列 的前
的前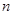 项和
项和 .
.
(1)求数列 的通项公式;
的通项公式;
(2)证明:对任意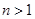 ,都有
,都有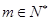 ,使得
,使得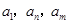 成等比数列.
成等比数列.