如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在直线CD上有一点P．
（1）如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD有怎样的数量关系？请说明理由．
（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？
如图，O是△ABC内任意一点，连接OB、OC．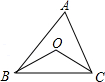
（1）求证：∠BOC＞∠A；
（2）比较AB+AC与OB+OC的大小，并说明理由．
如图，已知Rt△ABC≌Rt△ADE，∠ABC=∠ADE=90°，BC与DE相交于点F，连接CD，EB．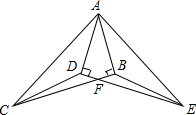
（1）图中还有几对全等三角形，请你一一列举；
（2）求证：CF=EF．
如图，在△ABC中，∠B=40°，∠C=60°，AD⊥BC于D，AE是∠BAC的平分线．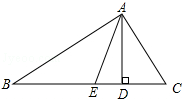
（1）求∠DAE的度数；
（2）写出以AD为高的所有三角形．
如图所示，将长方形ABCD沿DE折叠，使点C恰好落在BA边上，得到点C′，若∠C′EB=40°，求∠EDC′的度数．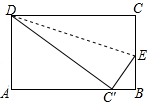
一个多边形的外角和是内角和的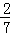
，求这个多边形的边数．