已知 是
是 内任意一点,连结
内任意一点,连结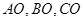 并延长交对边于
并延长交对边于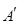 ,
, ,
,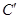 ,则
,则 .这是平面几何的一个命题,其证明常常采用“面积法”:
.这是平面几何的一个命题,其证明常常采用“面积法”:  .
.
运用类比,猜想对于空间中的四面体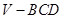 ,存在什么类似的结论,并用“体积法”证明.
,存在什么类似的结论,并用“体积法”证明.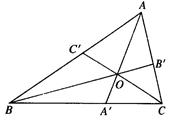
在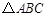 中,角
中,角 所对的边分别为
所对的边分别为 ,设
,设 为
为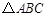 的面积,满足
的面积,满足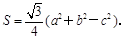
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)求 的最大值.
的最大值.
已知函数 ,的部分图象如图所示.
,的部分图象如图所示.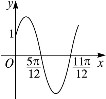
(Ⅰ)求函数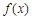 的解析式;
的解析式;
(Ⅱ)求函数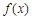 的单调递增区间.
的单调递增区间.
设函数 ,曲线
,曲线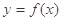 过点P(1,0),且在P点处的切斜线率为2.
过点P(1,0),且在P点处的切斜线率为2.
(1)求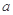 ,
, 的值;
的值;
(2)证明: .
.
某商场销售某种商品的经验表明,该商品每日的销售量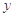 (单位:千克)与销售价格
(单位:千克)与销售价格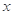 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式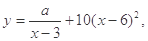 其中
其中 为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.
为常数.己知销售价格为5元/千克时,每日可售出该商品11千克.
(1)求 的值;
的值;
(2)若该商品的成本为3元/千克,试确定销售价格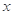 的值,使商场每日销售该商品所获得利润最大.
的值,使商场每日销售该商品所获得利润最大.
设△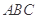 的内角
的内角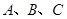 的对边分别为
的对边分别为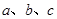 ,且
,且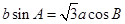 .
.
(1)求角 的大小;
的大小;
(2)若 ,
,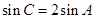 ,求a,c,的值.
,求a,c,的值.