如图,在四边形ABCD中,∠DAB=60º,AC平分∠DAB,BC⊥AC,AC与BD交于点E,AD=6,CE= ,
, ,求BC、DE的长及四边形ABCD的面积.
,求BC、DE的长及四边形ABCD的面积.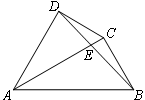
如图所示,CD⊥AB,垂足为D,点F是BC上任意一点,FE⊥AB,垂足为E,且∠CDG=∠BFE,∠AGD=80°,求∠BCA的度数.
如图所示,已知AC∥DE,∠1=∠2.求证:AB∥CD.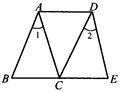
一个农妇要过河,随身携带一只小白兔、一篮萝卜和一只饥饿又爱追兔子的狗.她发现系在河边的小船一次只能载她本人和兔子、狗、萝卜其中之一过河,她不能让狗和兔子呆在一起(狗会吓坏可怜的小兔),也不能让小兔和萝卜留在一起(兔子会把萝卜全吃掉),怎么办?请你帮农妇想办法:她怎样来回渡河才能把三样东西安全带到对岸?
对于同一平面内的三条直线a,b,c,给出下列5个判断:①a∥b②b∥c;③a⊥b;④a∥c;⑤a⊥c.请以其中两个论断为条件,一个论断为结论,组成一个你认为正确的命题(至少写两个命题).
把下列命题改写成“如果……那么……”.
(1)两直线平行,同位角相等;
(2)在同一个三角形中,等角对等边;
(3)两边一夹角对应相等的两个三角形全等.