在平面直角坐标系xOy中，抛物线
经过原点O， 点B(-2，n)在这条抛物线上.
（1）求抛物线的解析式；
（2）将直线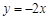
沿y轴向下平移b个单位后得到直线l， 若直线l经过B点，求n、b的值；
（3）在（2）的条件下，设抛物线的对称轴与x轴交于点C，直线l与y轴交于点D，且与抛物线的对称轴交于点E.若P是抛物线上一点，且PB=PE，求P点的坐标.
如图，在矩形OABC中，点B的坐标为（－2，3）。画出矩形OABC绕点O顺时针旋转90°后的矩形OA1B1C1,并直接写出的坐标A1、B1、C1的坐标。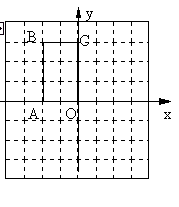
计算：（每小题8分，共16分）
（1）化简：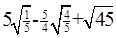
（2）解方程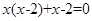
如图，DE是△ABC边AB的垂直平分线，分别交AB、BC于D、E。AE平分∠BAC. 设∠B = x（单位：度），∠C = y（单位：度）.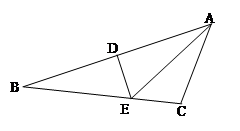
（1）求y随x变化的函数关系式，并写出自变量x的取值范围；
（2）请讨论当△ABC为等腰三角形时，∠B为多少度？
某公路的同一侧有A、B两个村庄，若以公路所在的直线为x轴建立平面直角坐标系，A、B两点的坐标分别为（1，2）、（4，1），如图所示。要在公路边上（即x轴）建一仓库，把货物运往A、B两地。试问：在公路边上是否存在一点C，使运货的路程最短。若存在，求出C点的坐标；若不存在，请说明理由。（要求写出运算过程）
已知：m2 = n+2，n2 = m+2（m≠n）.求：m2 +2mn+n2的值.