某公路的同一侧有A、B两个村庄，若以公路所在的直线为x轴建立平面直角坐标系，A、B两点的坐标分别为（1，2）、（4，1），如图所示。要在公路边上（即x轴）建一仓库，把货物运往A、B两地。试问：在公路边上是否存在一点C，使运货的路程最短。若存在，求出C点的坐标；若不存在，请说明理由。（要求写出运算过程）
已知如图，AB和DE是直立在地面上的两根
立柱，AB＝10m，
某一时刻AB在太阳光下的投影BC＝6m.
（1）请你在图中画出此时DE在阳光下的投影.
（2）在测量AB的投影时，同时测量出DE在阳光下的投影长为3m，计算DE的长.
某校九年级数学兴趣小组的同学开展了测量湘江宽度的活动．
如图，他们在河东岸边的
点测得河西岸边的标志物
在它的正西方向，然后从点出发沿河岸向正北方向行进550米到点
处，测得在点的南偏西60°方向上，他们测得的湘江宽度是多少米？
（结果保留整数，参考数据：
，
）
抛物线的顶点坐标为（2，－3），且过点（－1，7），求这条抛物线的解析式
在Rt△ABC中，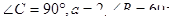
，求b、
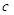与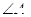
四边形ABCD各顶点的坐标分别为A（1，3）、B（5，2）、C（8，4）、D（6，9），
以原点为位似中心，相似比为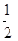
的位似图形A1B1C1D1，且四边形A1B1C1D1在第一象限。
写出各点坐标。