已知函数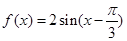
，
.
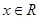（1）写出函数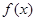
的周期；
（2）将函数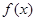图象上的所有的点向左平行移动
个单位,得到函数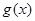
的图象,写出函数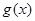的表达式,并判断函数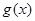的奇偶性.
已知
为椭圆
的左，右焦点，
为椭圆上的动点，且
的最大值为1，最小值为-2.
（I）求椭圆
的方程；
（II）过点
作不与
轴垂直的直线
交该椭圆于
两点，
为椭圆的左顶点。试判断
的大小是否为定值，并说明理由.
如图，已知长方形
中，
,
为
的中点. 将
沿
折起，使得平面
平面
.
（I）求证：
；
（II）若点
是线段
的中点，求二面角
的余弦值.
为了解甲、乙两厂的产品质量，采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取12件和5件，测量产品中微量元素x，y的含量（单位：毫克）.下表是乙厂的5件产品的测量数据：
| 编号 |
1 |
2 |
3 |
4 |
5 |
| x |
169 |
178 |
166 |
175 |
180 |
| y |
75 |
80 |
77 |
76 |
81 |
（1）已知甲厂生产的产品共84件，求乙厂生产的产品数量；
（2）当产品中的微量元素x，y满足x≥175且y≥75，该产品为优等品，
①用上述样本数据估计乙厂生产的优等品的数量；
②从乙厂抽出的上述5件产品中，随机抽取2件，求抽取的2件产品中优等品数
的分布列及其期望．
已知点A（4，0）、B（0，4）、C（
）
（1）若
，且
，求
的大小；
（2）
，求
的值．
已知
，
R
（Ⅰ）当
时，解不等式
；
（Ⅱ）若
恒成立，求k的取值范围.