正方形网格中，小格的顶点叫做格点，以格点为顶点的三角形叫做格点三角形．下图1中的正方形网格中△ABC是格点三角形，小正方形网格的边长为1(单位长度)．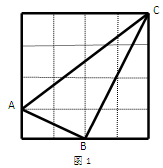
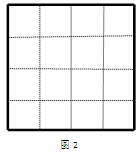
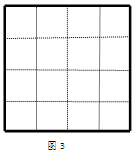
(1) △ABC的面积是 (平方单位)；
(2)在图2所示的正方形网格中作出格点△A′B′C′和△A″B″C″，使△A′B′C′∽△ABC，△A″B″C″∽△ABC，且AB、A′B′、A″B″中任意两条线段的长度都不相等；
(3)在所有与△ABC相似的格点三角形中，是否存在面积为3(平方单位)的格点三角形？如果存在，请在图3中作出，如果不存在，请说明理由．
在△ABC中，AB=AC，点D在边BC所在的直线上，过点D作DF∥AC交直线AB于点F，DE∥AB交直线AC于点E．
（1）当点D在边BC上时，如图①，求证：DE+DF=AC．
（2）当点D在边BC的延长线上时，如图②；当点D在边BC的反向延长线上时，如图③，请分别写出图②、图③中DE，DF，AC之间的数量关系，不需要证明．
（3）若AC=6，DE=4，则DF= ．
快、慢两车分别从相距360千米路程的甲、乙两地同时出发，匀速行驶，先相向而行，快车到达乙地后，停留1小时，然后按原路原速返回，快车比慢车晚1小时到达甲地，快、慢两车距各自出发地的路程y（千米）与出发后所用的时间x（小时）的关系如图所示．
请结合图象信息解答下列问题：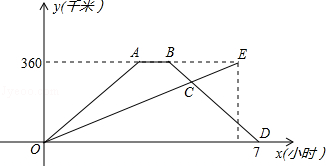
（1）快、慢两车的速度各是多少？
（2）出发多少小时，快、慢两车距各自出发地的路程相等？
（3）直接写出在慢车到达甲地前，快、慢两车相距的路程为150千米的次数．
某校为了了解学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机抽取了本校部分学生进行问卷调查（必选且只选一类节目），将调查结果进行整理后，绘制了如下不完整的条形统计图和扇形统计图，其中喜爱体育节目的学生人数比喜爱戏曲节目的学生人数的3倍还多1人．
请根据所给信息解答下列问题：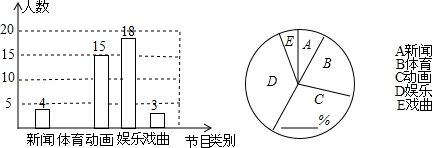
（1）求本次抽取的学生人数．
（2）补全条形图，在扇形统计图中的横线上填上正确的数值，并直接写出“体育”对应的扇形圆心角的度数．
（3）该校有3000名学生，求该校喜爱娱乐节目的学生大约有多少人？
矩形ABCD的对角线AC，BD相交于点O，AC=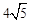
，BC=4，向矩形ABCD外作△CDE，使△CDE为等腰三角形，且点E在边BC所在的直线上，请你画出图形，直接写出OE的长，并画出体现解法的辅助线．
如图，直线MN与x轴，y轴分别相交于A，C两点，分别过A，C两点作x轴，y轴的垂线相交于B点，且OA，OC（OA＞OC）的长分别是一元二次方程x2﹣14x+48=0的两个实数根．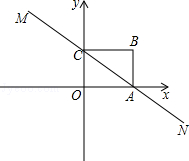
（1）求C点坐标；
（2）求直线MN的解析式；
（3）在直线MN上存在点P，使以点P，B，C三点为顶点的三角形是等腰三角形，请直接写出P点的坐标．