已知：A(a，y1)、B(2a，y2)是反比例函数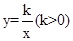
图像上的两点．
(1)比较y1与y2的大小关系；
(2)若A、B两点在一次函数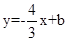
第一象限的图像上(如图所示)，分别过A、B两点作x轴的垂线，垂足分别为C、D，连结OA、OB，且S△OAB=8，求a的值；
(3)在(2)的条件下，如果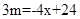
，
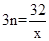，求使得m>n的x的取值范围．
如图，在△ABC中，AB=AC=8cm，∠BAC=120°．
（1）作△ABC的外接圆（只需作出图形，并保留作图痕迹）；
（2）求它的外接圆半径．
如图，在直角坐标平面内，直线y=－x+5与
轴和
轴分别交于A、B两点，二次函数y=
+bx+c的图象经过点A、B，且顶点为C．
（1）求这个二次函数的解析式；
（2）求sin∠OCA的值；
（3）若P是这个二次函数图象上位于x轴下方的一点，且
ABP的面积为10，求点P的坐标．
如图在Rt△ABC中，∠C＝90°，点D是AC的中点，且∠A＋∠CDB＝90°，过点A、D作⊙O，使圆心O在AB上，⊙O与AB交于点E．
（1）求证：直线BD与⊙O相切；
（2）若AD：AE＝4：5，BC＝6，求⊙O的直径．
如图，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，若∠PAB=40°，求∠P的度数．
居民区内的“广场舞”引起媒体关注，辽宁都市频道为此进行过专访报道．小平想了解本小区居民对“广场舞”的看法，进行了一次抽样调查，把居民对“广场舞”的看法分为四个层次：A：非常赞同；B：赞同但要有时间限制；C：无所谓；D：不赞同．并将调查结果绘制了图1和图2两幅不完整的统计图．
请你根据图中提供的信息解答下列问题：
（1）求本次被抽查的居民有多少人？
（2）将图1和图2补充完整；
（3）求图2中“C”层次所在扇形的圆心角的度数；
（4）估计该小区4000名居民中对“广场舞”的看法表示赞同（包括A层次和B层次）的大约有多少人．