如图，直线l上摆放着两块大小相同的直角三角形△ABC和△ECD，∠ACB=∠DCE=90°，且BC=CE=3，AC=CD=4，将△ECD绕点C逆时针旋转到△E1CD1位置，且D1E1∥l ，则B、E1两点之间的距离为（ ）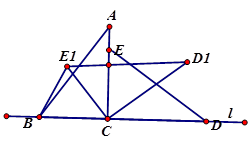
A.3 B.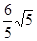
C. 
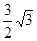D.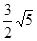 
若把不等式组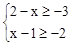
的解集在数轴上表示出来，则其对应的图形为
| A．长方形 | B．线段 | C．射线 | D．直线 |
对于任意实数k，关于x的方程
的根的情况为
| A．有两个相等的实数根 | B．没有实数根 |
| C．有两个不相等的实数根 | D．无法确定 |
若从长度分别为3、5、6、9的四条线段中任取三条，则能组成三角形的概率为
A． |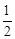
B． |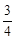
C． |
D． |
如图，等边△ABC沿射线BC向右平移到△DCE的位置，连接AD、BD，则下列结论：①AD=BC；②BD、AC互相平分；③四边形ACED是菱形．其中正确的个数是
A．0 B．1 C．2 D．3
若正方形的边长为6，则其外接圆半径与内切圆半径的大小分别为
A．6， |
B．，3 |
C．6，3 | D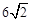． ， |