如图,在四棱锥P-ABCD中,底面是边长为2 的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=
的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=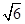 ,M,N分别为PB,PD的中点.
,M,N分别为PB,PD的中点.

(1)证明:MN∥平面ABCD;
(2) 过点A作AQ⊥PC,垂足为点Q,求二面角A-MN-Q的平面角的余弦值.
函数 (其中
(其中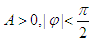 )的图象如图所示,把函数
)的图象如图所示,把函数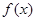 的图像向右平移
的图像向右平移 个单位,再向下平移1个单位,得到函数
个单位,再向下平移1个单位,得到函数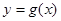 的图像.
的图像.
(1)若直线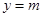 与函数
与函数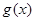 图像在
图像在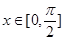 时有两个公共点,其横坐标分别为
时有两个公共点,其横坐标分别为 ,求
,求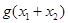 的值;
的值;
(2)已知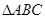 内角
内角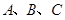 的对边分别为
的对边分别为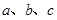 ,且
,且
 .若向量
.若向量 与
与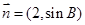 共线,求
共线,求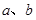 的值.
的值.
已知函数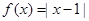
(1)解不等式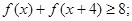
(2)若 .求证:
.求证: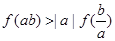 .
.
在直角坐标系中,曲线C的参数方程为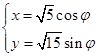 (
(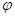 为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,点
为参数).以原点为极点,x轴的正半轴为极轴建立极坐标系,点 ,直线l的极坐标方程为
,直线l的极坐标方程为 .
.
(1)判断点P与直线l的位置关系,说明理由;
(2)设直线l与曲线C的两个交点为A、B,求 的值.
的值.
已知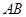 为半圆
为半圆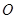 的直径,
的直径, ,
,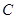 为半圆上一点,过点
为半圆上一点,过点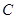 作半圆的切线
作半圆的切线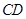 ,过点
,过点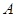 作
作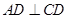 于
于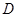 ,交圆于点
,交圆于点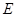 ,
, .
.
(Ⅰ)求证: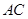 平分
平分 ;
;
(Ⅱ)求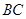 的长.
的长.
已知函数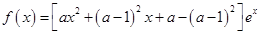 (其中
(其中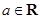 ).
).
(Ⅰ)若 为
为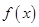 的极值点,求
的极值点,求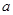 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,解不等式 ;
;
(Ⅲ)若函数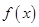 在区间
在区间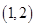 上单调递增,求实数
上单调递增,求实数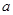 的取值范围.
的取值范围.