甲,乙两人进行乒乓球比赛,约定每局胜者得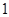 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时停止.设甲在每局中获胜的概率为
局时停止.设甲在每局中获胜的概率为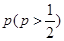 ,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为
,且各局胜负相互独立.已知第二局比赛结束时比赛停止的概率为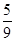 .
.
(Ⅰ)求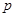 的值;
的值;
(Ⅱ)设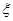 表示比赛停止时比赛的局数,求随机变量
表示比赛停止时比赛的局数,求随机变量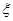 的分布列和数学期望
的分布列和数学期望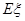 .
.
若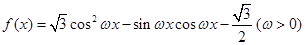 的图像与直线
的图像与直线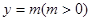 相切,并且切点横坐标依次成公差为
相切,并且切点横坐标依次成公差为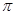 的等差数列.
的等差数列.
(1)求 和
和 的值;
的值;
(2)在⊿ABC中,a、b、c分别是∠A、∠B、∠C的对边.若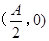 是函数
是函数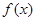 图象的一个对称中心,且a=4,求⊿ABC外接圆的面积.
图象的一个对称中心,且a=4,求⊿ABC外接圆的面积.
设a为实数,函数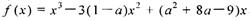 ,x
,x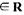
 (1) 当a= 0时,求
(1) 当a= 0时,求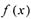 的极大值、极小值;
的极大值、极小值;
(2) 若x>0时,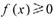 ,求a的取值范围;.
,求a的取值范围;.
(3) 若函数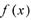 在区间(0,1)上是减函数,求a的取值范围.
在区间(0,1)上是减函数,求a的取值范围.
已知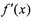 是函数
是函数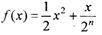 (
( )的导函数,数列{
)的导函数,数列{ }满足
}满足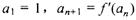 .
.
(1) 求数列{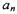 }的通项公式;
}的通项公式;
(2) 若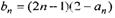 ,
,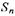 为数列{
为数列{ }的前n项和,求
}的前n项和,求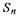
设椭圆C: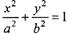 (“a>b〉0)的左焦点为
(“a>b〉0)的左焦点为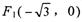 ,椭圆过点P(
,椭圆过点P(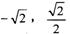 )
)
(1)求椭圆C的方程;
(2)已知点D(1, 0),直线l: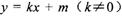 与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.