解答一个问题后，将结论作为条件之一，提出与原问题有关的新问题，我们把它称为原问题的一个“逆向”问题．例如，原问题是“长方形的长和宽的长分别是3和4，求长方形的周长”，求出周长等于14后，它的一个“逆向”问题可以是“若长方形的周长为14，且一边长为3，求另一边的长”；也可以是“若长方形的周长为14，求长方形面积的最大值”，等等．
（1）设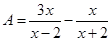
，
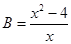，求A与B的积；
（2）提出（1）的一个“逆向”问题，并解答这个问题．
为宣传节约用水，小明随机调查了某小区部分家庭5月份的用水情况，并将收集的数据整理成如下统计图．
（1）小明一共调查了多少户家庭？
（2）求所调查家庭5月份用水量的众数、平均数；
（3）若该小区有400户居民，请你估计这个小区5月份的用水量．
观察下列图形的变化过程，解答以下问题：
如图，在△ABC中，D为BC边上的一动点（D点不与B、C两点重合）．DE∥AC交AB于E点，DF∥AB交AC于F点．
（1）试探索AD满足什么条件时，四边形AEDF为菱形，并说明理由；
（2）在（1）的条件下，△ABC满足什么条件时，四边形AEDF为正方形．为什么？
已知：在平面直角坐标系中，点A（1，0），点B（4，0），点C在y轴正半轴上，且OB=2OC．
（1）试确定直线BC的解析式；
（2）在平面内确定点M，使得以点M、A、B、C为顶点的四边形是平行四边形，请直接写出点M的坐标．
已知m，n，d为一个直角三角形的三边长，且有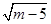
=8n﹣n2﹣16，求三角形三边长分别为多少？
（1）某水果批发商，批发苹果不少于80kg时，批发价为2.5元/kg，小张携现金2500元到这个市场采购苹果，并以批发价买进，设购买的苹果为xkg，小张付款后还剩余现金y元，写出y与x的函数关系式，并指出自变量x的取值范围．
（2）在直角坐标系中，直接画出函数y=|x+1|的图象．