下列图表是某校今年参加中考体育的男生1000米跑、女生800米跑的成绩中分别抽取的10个数据．
| 考 生 编 号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
| 男 生 成 绩 |
3′05〞 |
3′11〞 |
3′53〞 |
3′10〞 |
3′55〞 |
3′30〞 |
3′25〞 |
3′19〞 |
3′27〞 |
3′55〞 |
（1）求出这10名女生成绩的中位数、众数和极差；
（2）按规定，男生1000米跑成绩不超过3′35〞就可以得满分．该校学生有490人，男生比女生少70人． 请你根据上面抽样的结果，估算该校考生中有多少名男生该项考试得满分？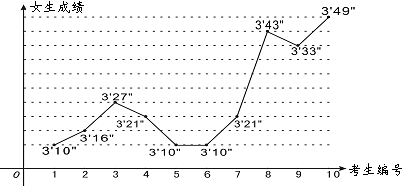
先化简在求值：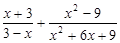
，其中
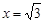
计算： 
如图，抛物线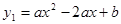
的顶点为D，与x轴交于点A，B，与y轴交于点C，且OB =" 2OC=" 3．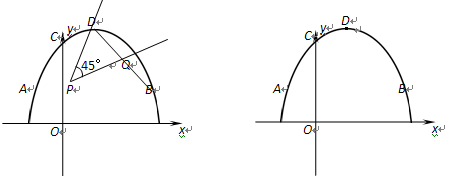
（1）求a，b的值；
（2）将45°角的顶点P在线段OB上滑动(不与点B重合)，该角的一边过点D，另一边与BD交于点Q，设P（x，0），y2=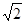
DQ，试求出y2关于x的函数关系式；
（3）在同一平面直角坐标系中，两条直线x = m，x = m+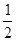
分别与抛物线y1交于点E，G，与y2的函数图象交于点F，H．问点E、F、H、G围成四边形的面积能否为
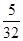？若能，求出m的值；若不能，请说明理由．
△ABC中，∠A=90°，点D在线段BC上（端点B除外），∠EDB =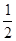 
∠C，BE⊥DE于点E，DE与AB相交于点F．
（1）当AB = AC时（如图1）
①∠EBF= ▲ °；
②小明在探究过程中发现，线段FD 与BE始终保持一种特殊的数量关系，请你猜想这个关系，并利用所学知识证明猜想的正确性；
（2）探究：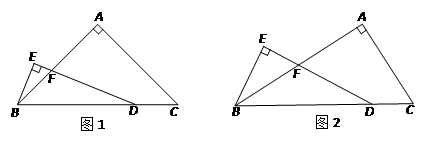
当AB = kAC时（k＞0，如图2），用含k的式子表示线段FD与BE之间的数量关系，请直接写出结果．
如图，C为以AB为直径的⊙O上一点，AD和过点C的切线互相垂直，垂足为点D．
（1）求证：AC平分∠BAD；
（2）若CD
3，AC=3
，求⊙O的半径长．