为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,抽样调查了50名学生参加户外活动的时间,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题: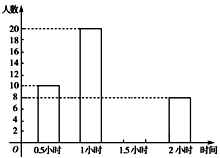
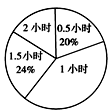
(1)补充户外活动时间为1.5小时的频数分布直方图;
(2)求表示户外活动时间 1小时的扇形圆心角的度数;
(3)户外活动时间的中位数是多少?
(4)本次调查中学生参加户外活动的平均时间是否符合要求?
如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).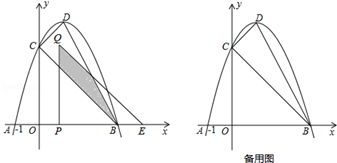
(1)求点B,C的坐标;
(2)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
某商店欲购进甲、乙两种商品,已知甲的进价是乙的进价的一半,进3件甲商品和1件乙商品恰好用200元.甲、乙两种商品的售价每件分别为80元、130元,该商店决定用不少于6710元且不超过6810元购进这两种商品共100件.
(1)求这两种商品的进价.
(2)该商店有几种进货方案?哪种进货方案可获得最大利润,最大利润是多少?
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.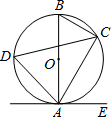
(1)求证:AE是⊙O的切线
(2)当BC=4时,求劣弧AC的长
如图,已知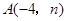 ,
,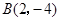 是一次函数
是一次函数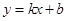 的图象和反比例函数
的图象和反比例函数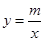 的图象的两个交点.
的图象的两个交点.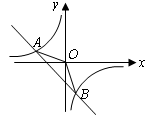
(1)求反比例函数和一次函数的解析式;
(2)求△ 的面积;
的面积;
今年西宁市高中招生体育考试测试管理系统的运行,将测试完进行换算统分改为计算机自动生成,现场公布成绩,降低了误差,提高了透明度,保证了公平.考前张老师为了解全市初三男生考试项目的选择情况(每人限选一项),对全市部分初三男生进行了调查,将调查结果分成五类:A、实心球(2kg);B、立定跳远;C、50米跑;D、半场运球;E、其它.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: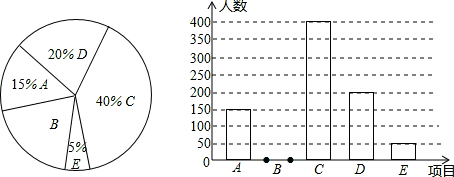
(1)将上面的条形统计图补充完整;
(2)假定全市初三毕业学生中有5500名男生,试估计全市初三男生中选50米跑的人数有多少人?
(3)甲、乙两名初三男生在上述选择率较高的三个项目:B、立定跳远;C、50米跑;D、半场运球中各选一项,同时选择半场运球、立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果.