在O点固定一个长度为L的轻质不可伸长的细绳,绳子的另一端连接一个质量为m的小球,当绳子与竖直方向为 时,小球以
时,小球以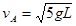 的垂直于绳子的速度在A点释放,它绕O点在竖直面内做圆周运动,重力加速度为g,求:
的垂直于绳子的速度在A点释放,它绕O点在竖直面内做圆周运动,重力加速度为g,求:
(1)小球到最低点B点时速度大小
(2)小球到最低点B点时,绳子的拉力F1
(3)小球到最高点c时,绳子的拉力F2
某弹性小球从距地面高度H处静止下落,假设小球与地面发生弹性碰撞(没有损失能量),但由于恒定大小的空气阻力的影响,小球只能上升H.现为了使小球与地面碰撞后还能上升原来的高度H,则必须给小球多大的初速度v0?
如图所示,光滑水平地面静止放着质量m=10 kg的木箱,与水平方向成θ=60°的恒力F作用于物体,恒力F=2.0 N.当木箱在力F作用下由静止开始运动4.0 s后,求:
4.0 s末物体的速度大小;
4s内力F所做的功;
4.0 s末力F的瞬时功率
如图,竖直放置的均匀U形管一端封闭,在温度为27℃时封闭有57cm长的空气,大气压为76cmHg,两管中水银面高度差为38cm,求:气体温度升高到多少K时两管中水银面正好相平? 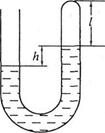
图为示波管的示意图,竖直偏转电极的极板长l=4.0 cm,两板间距离d=1.0 cm,极板 右端与荧光屏的距离L=18 cm。由阴极发出的电子经电场加速后,以
右端与荧光屏的距离L=18 cm。由阴极发出的电子经电场加速后,以 v=1.6×107 m/s的速度沿中心线进入竖直偏转电场。若电子由阴极逸出时的初速度、电子所受重力及电子之间的相互作用力可忽略不计,已知电子的电荷量e=1.6×10-19 C,质量m=0.91×10-30 kg。
v=1.6×107 m/s的速度沿中心线进入竖直偏转电场。若电子由阴极逸出时的初速度、电子所受重力及电子之间的相互作用力可忽略不计,已知电子的电荷量e=1.6×10-19 C,质量m=0.91×10-30 kg。
求加速电压U0的大小;
要使电子束不打在偏转电极的极板上,求加在竖直偏转电极上的电压应满足的条件;
在竖直偏转电极上加u=40 sin100πt(V)的交变电压,求电子打在荧光屏上亮线的长度。
航模兴趣小组设计出一架遥控飞行器,其质量m =2㎏,动力系统提供的恒定升力F ="28" N。试飞时,飞行器从地面由静止开始 竖直上升。设飞行器飞行时所受的阻力大小不变,g取10m/s2。
竖直上升。设飞行器飞行时所受的阻力大小不变,g取10m/s2。第一次试飞,飞行器飞行t1 =" 8" s 时到达高度H =" 64" m。求飞行器所阻力f的大小;
第二次试飞,飞行器飞行t2 =" 6" s 时遥控器出现故障,飞行器立即失去升力。求飞行器
 能达到的最大高度h;
能达到的最大高度h;为了使飞行器不致坠落到地面,求飞行器从开始下落到恢复升力的最长时间t3。