科幻小说《实验室的故事》中,有这样一个情节,科学家把一种珍奇的植物分别放在不同温度的环境中,经过一天后,测试出这种植物高度的增长情况(如下表):
温度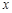 /℃ /℃ |
…… |
-4 |
-2 |
0 |
2 |
4 |
4.5 |
…… |
植物每天高度增长量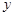 /mm /mm |
…… |
41 |
49 |
49 |
41 |
25 |
19.75 |
…… |
由这些数据,科学家推测出植物每天高度增长量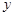 是温度
是温度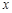 的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
的函数,且这种函数是反比例函数、一次函数和二次函数中的一种.
(1)请你选择一种适当的函数,求出它的函数关系式,并简要说明不选择另外两种函数的理由;
(2)温度为多少时,这种植物每天高度的增长量最大?
(3)如果实验室温度保持不变,在10天内要使该植物高度增长量的总和超过250mm,那么实验室的温度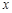 应该在哪个范围内选择?请直接写出结果.
应该在哪个范围内选择?请直接写出结果.
小明在做作业时,不慎将墨水滴在一个三项式上,将前后两项污染得看不清楚了,但中间项是12xy,为了便于填上后面的空,请你帮他把前后两项补充完整,使它成为完全平方式,你有几种方法?(至少写出三种不同的方法)
三项式:■+12xy+■= ( ) 2.
(1) ;(2) ;(3) .
我们知道因式分解与整式乘法是互逆的关系,那么逆用乘法公式(x+a)(x+b)=x2+(a+b)x+ab,即x2+(a+b)x+ab=(x+a)(x+b)是否可以分解因式呢?当然可以,而且也很简单.
如:
(1)x2+5x+6=x2+(3+2)x+3×2=(x+2)(x+3);
(2)x2﹣5x﹣6=x2+(﹣6+1)x+(﹣6)×1=(x﹣6)(x+1).
请你仿照上述方法,把下列多项式分解因式:
(1)x2﹣8x+7;
(2)x2+7x﹣18.
(1)8a3b2﹣12ab3c+6a3b2c
(2)8a(x﹣a)+4b(a﹣x)﹣6c(x﹣a)
(3)﹣x5y3+x3y5(4)4(a﹣b)2﹣16(a+b)2
(5)﹣8ax2+16axy﹣8ay2(6)m2+2n﹣mn﹣2m
(7)a2﹣4a+4﹣c2
(8)(a2+1)2﹣4a2
(9)(x+3y)2+(2x+6y)(3y﹣4x)+(4x﹣3y)2(10)a4﹣6a2﹣27.
对下列代数式分解因式
(1)a2(x﹣y)﹣4b2(x﹣y)
(2)a3+6a2+9a
(3) x4﹣1
(4) x2﹣7x+10
分解因式:
(1)x2y2﹣y2
(2)x2﹣4ax﹣5a2.
因式分解:(1)a4﹣5a2﹣36;(2)x2﹣4x+4﹣4y2