小明在做作业时,不慎将墨水滴在一个三项式上,将前后两项污染得看不清楚了,但中间项是12xy,为了便于填上后面的空,请你帮他把前后两项补充完整,使它成为完全平方式,你有几种方法?(至少写出三种不同的方法)
三项式:■+12xy+■= ( ) 2.
(1) ;(2) ;(3) .
我们知道因式分解与整式乘法是互逆的关系,那么逆用乘法公式(x+a)(x+b)=x2+(a+b)x+ab,即x2+(a+b)x+ab=(x+a)(x+b)是否可以分解因式呢?当然可以,而且也很简单.
如:
(1)x2+5x+6=x2+(3+2)x+3×2=(x+2)(x+3);
(2)x2﹣5x﹣6=x2+(﹣6+1)x+(﹣6)×1=(x﹣6)(x+1).
请你仿照上述方法,把下列多项式分解因式:
(1)x2﹣8x+7;
(2)x2+7x﹣18.
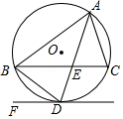
如图, 是 的外接圆, 的平分线交 于点 ,交 于点 ,过点 作直线 .
(1)判断直线 与 的位置关系,并说明理由;
(2)若 , , ,求 的长.
端午节前后,张阿姨两次到超市购买同一种粽子.节前,按标价购买,用了96元;节后,按标价的6折购买,用了72元,两次一共购买了27个.这种粽子的标价是多少?
如图,在 中, , , .
(1)尺规作图:不写作法,保留作图痕迹.
①作 的平分线,交斜边 于点 ;
②过点 作 的垂线,垂足为点 .
(2)在(1)作出的图形中,求 的长.
随机抽取某小吃店一周的营业额(单位:元)如下表:
|
星期一 |
星期二 |
星期三 |
星期四 |
星期五 |
星期六 |
星期日 |
合计 |
|
540 |
680 |
640 |
640 |
780 |
1110 |
1070 |
5460 |
(1)分析数据,填空:这组数据的平均数是 元,中位数是 元,众数是 元.
(2)估计一个月的营业额(按30天计算)
①星期一到星期五营业额相差不大,用这5天的平均数估算合适么?
答(填“合适”或“不合适” .
②选择一个你认为最合适的数据估算这个小吃店一个月的营业额.
先化简: ,再选取一个适当的 的值代入求值.