如图，点P是直线
：
上的点，过点P的另一条直线
交抛物线
于A、B两点．
（1）若直线的解析式为
，求A、B两点的坐标；
（2）①若点P的坐标为（－2，
），当PA＝AB时，请直接写出点A的坐标；
②试证明：对于直线上任意给定的一点P，在抛物线上都能找到点A，使得PA＝AB成立．
（3）设直线交
轴于点C，若△AOB的外心在边AB上，且∠BPC＝∠OCP，求点P的坐标．
如图，△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB与AC、AE分别交于点O、点E，连接EC．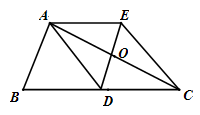
（1）求证：AD=EC；
（2）当∠BAC=90°时，求证：四边形ADCE是菱形；
甲、乙两名同学进行射击训练，在相同条件下各射靶5次，成绩统计如下：
| 命中环数 |
7 |
8 |
9 |
10 |
| 甲命中环数的次数 |
2 |
2 |
0 |
1 |
| 乙命中环数的次 |
1 |
3 |
1 |
0 |
若从甲、乙两人射击成绩方差的角度评价两人的射击水平，则谁的射击成绩更稳定
些？
某班将买一些乒乓球和乒乓球拍，现了解情况如下：甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍．乒乓球拍每副定价30元，乒乓球每盒定价5元．经洽谈后，甲店每买一副球拍赠一盒乒乓球，乙店全部按定价的9折优惠．该班需球拍5副，乒乓球若干盒（不小于5盒）．问：（1）当购买乒乓球多少盒时，两种优惠办法付款一样？
（2）当购买15盒、30盒乒乓球时，请你去办这件事，你打算去哪家商店购买？为什么？
探索规律：观察下面由※组成的图案和算式，并解答问题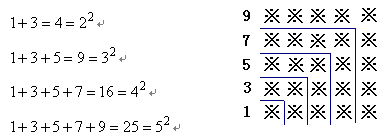
（
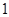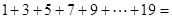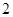）试猜想
；（
）试猜想
=； （
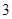）请用上述规律计算：
（请算出最后数值哦！）