如图所示,光滑水平面AB与竖直面的半圆形导轨在B点相连接,导轨半径为R,一个质量为m的静止的木块在A处压缩弹簧,释放后,木块获得向右的初速度,当它经过B点进入半圆形导轨瞬间对导轨的压力是其重力的7倍,之后向上运动恰能通过轨道最高点C,试求: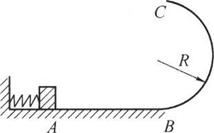
(1)木块到达B处时的速度大小;
(2)木块释放前,弹簧所具有的弹性势能;
(3)木块从B到C过程中克服摩擦力所做的功。
如图所示,一个质量m=1kg的长木板静止在光滑的水平面上,并与半径为R=1.8m的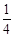 光滑圆弧形固定轨道接触(但不粘连),木板的右端到竖直墙的距离为s=0.08m;另一质量也为m的小滑块从轨道的最高点由静止开始下滑,从圆弧的最低点A滑上木板。设长木板每次与竖直墙的碰撞时间极短且无机械能损失。木板的长度可保证物块在运动的过程中不与墙接触。已知滑块与长木板间的动摩擦因数
光滑圆弧形固定轨道接触(但不粘连),木板的右端到竖直墙的距离为s=0.08m;另一质量也为m的小滑块从轨道的最高点由静止开始下滑,从圆弧的最低点A滑上木板。设长木板每次与竖直墙的碰撞时间极短且无机械能损失。木板的长度可保证物块在运动的过程中不与墙接触。已知滑块与长木板间的动摩擦因数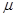 =0.1,g取10m/s2。试求:
=0.1,g取10m/s2。试求: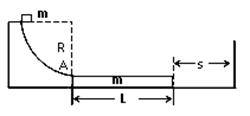
(1)滑块到达A点时对轨道的压力大小;
(2)当滑块与木板达到共同速度(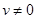 )时,滑块距离木板左端的长度是多少?
)时,滑块距离木板左端的长度是多少?
如图所示,质量为m的小物块在粗糙水平桌面上做直线运动,经距离l后以速度v飞离桌面,最终落在水平地面上。已知l=1.4m,v=3.0m/s,m=0.10kg,物块与桌面间的动摩擦因数 =0.25,桌面高h=0.45m,不计空气阻力,重力加速度g取10m/s2.求:
=0.25,桌面高h=0.45m,不计空气阻力,重力加速度g取10m/s2.求:
(1)小物块落地点距飞出点的水平距离s;
(2)小物块的初速度大小v0.
某校物理兴趣小组决定举行遥控赛车比赛。比赛路径如图所示,赛车从起点A出发,沿水平直线轨道运动L后,由B点进入半径为R的光滑竖直圆轨道,离开竖直圆轨道后继续在光滑平直轨道上运动到C点,并能越过壕沟。已知赛车质量m=0.1kg,通电后以额定功率P=1.5w工作,进入竖直轨道前受到阻力恒为0.3N,随后在运动中受到的阻力均可不记。图中L=10.00m,R=0.32m,h=1.25m,S=1.50m。问:要使赛车完成比赛,电动机至少工作多长时间?(取g=10m/s2)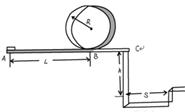
中子星是恒星演化过程的一种可能结果,它的密度很大。现有一中子星,观测到它的自转周期为T= s。问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.67
s。问该中子星的最小密度应是多少才能维持该星的稳定,不致因自转而瓦解。计算时星体可视为均匀球体。(引力常数G=6.67 10
10 m
m /kg.s
/kg.s )
)
甲、乙两个同学在直跑道上进行4×100 m接力(如图所示),他们在奔跑时有相同的最大速度,乙从静止开始全力奔跑需跑出25 m才能达到最大速度,这一过程可看作匀加速直线运动.现在甲持棒以最大速度向乙奔来,乙在接力区伺机全力奔出.若要求乙接棒时奔跑的速度达到最大速度的80%,则:
(1)乙在接力区须奔出多少距离?
(2)乙应在距离甲多远时起跑?