为了保护环境，某企业决定购买10台污水处理设备．现有A、B两种型号的设备，其中每台的价格、月处理污水量及年消耗费如右表：经预算，该企业购买设备的资金不高于105万元．
| |
A型 |
B型 |
| 价格（万元/台） |
12 |
10 |
| 处理污水量（吨/月） |
240 |
200 |
| 年消耗费（万元/台） |
1 |
1 |
（1）请你设计该企业有几种购买方案；
（2）若企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案；
（3）在第（2）问的条件下，若每台设备的使用年限为10年，污水厂处理污水费为每吨10元，请你计算，该企业自己处理污水与将污水排到污水厂处理相比较，10年节约资金多少万元？（注：企业处理污水的费用包括购买设备的资金和消耗费）.
工厂有一批长3dm、宽2dm的矩形铁片，为了利用这批材料，在每一块上裁下一个最大的圆铁片⊙O1之后（如图所示），再在剩余铁片上裁下一个充分大的圆铁片⊙O2．（1）求⊙O1、⊙O2的半径r1、r2的长；
（2）能否在剩余的铁片上再裁出一个与⊙O2同样大小的圆铁片？为什么？
已知函数y1＝－
x2 和反比例函数y2的图象有一个交点是 A（
，－1）．（1）求函数y2的解析式；
（2）在同一直角坐标系中，画出函数y1和y2的图象草图；
（3）借助图象回答：当自变量x在什么范围内取值时，对于x的同一个值，都有y1＜y2？
口袋里有 5枚除颜色外都相同的棋子，其中 3枚是红色的，其余为黑色．（1）从口袋中随机摸出一枚棋子，摸到黑色棋子的概率是_______ ；
（2）从口袋中一次摸出两枚棋子，求颜色不同的概率．（需写出“列表”或画“树状图”的过程）
如图，在由小正方形组成的12×10的网格中，点O、M和四边形ABCD的顶点都在格点上．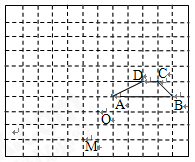
（1）画出与四边形ABCD关于直线CD对称的图形；
（2）平移四边形ABCD，使其顶点B与点M重合，画出平移后的图形；
（3）把四边形ABCD绕点O逆时针旋转90°，画出旋转后的图形．
已知二次函数 y＝ax2－x＋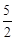
的图象经过点（－3, 1）．
（1）求 a 的值；
（2）判断此函数的图象与x轴是否相交？如果相交，请求出交点坐标；
（3）画出这个函数的图象．（不要求列对应数值表，但要求尽可能画准确）